noi.ac-CSP模拟Day5T2 灯

算是一道思维题吧，没有什么算法在里面。

之前想的是，能走的话就尽量走远，走过去开灯然后再回去关灯，然后再走，每一段路要走3次。

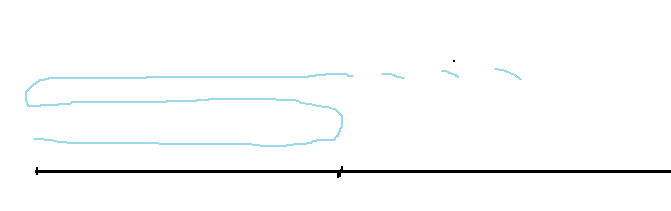
然而，“能走的话就尽量走远”只是yy的一个贪心，没有任何依据。假设在中间找一个过渡点的话，路程应该是长这个样子的：

总路程还是3倍距离，没有改变诶。

所以只要你认认真真地，正正常常地走路，不绕圈圈，所走的路程都是3倍距离。

所以只需要判断能不能走到就可以了。

既然如此，那就可以随便开灯了（大雾）

（没有开玩笑啊）是真的可以随便开灯了，因为只是要判断能否走到，就用不着节约了。

从左走到右的时候，依次开灯，每次开灯之后要保证至少走到下一个点
回去的时候不用管
再一次从左走到右关灯，这一次走的时候依靠的是前面没有被关的灯光
前面延伸到左边最远的灯光要保证自己所在的位置有灯

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<string>
 #include<queue>
 #include<algorithm>
 #include<vector>
 #include<cstdlib>
 using namespace std;
 #define N 300005
 #define ll long long
 #define INF 0x3f3f3f3f
 int n;
 int p[N],r[N];
 /*
 从左走到右的时候，依次开灯，每次开灯之后要保证至少走到下一个点
 回去的时候不用管
 再一次从左走到右关灯，这一次走的时候依靠的是前面没有被关的灯光
 前面延伸到左边最远的灯光要保证自己所在的位置有灯
 */
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
         scanf("%d %d",&p[i],&r[i]);
     int far=p[];//能够延伸到右边最远的灯光坐标 保证能够走到终点
     for(int i=;i<=n;i++)
     {
         far=max(far,p[i-]+r[i-]);
         if(far<p[i])
         {
             puts("-1");
             return ;
         }
     }
     far=p[n];//能够延伸到左边最远的灯光坐标 保证能够关灯
     for(int i=n;i>=;i--)
     {
         far=min(far,p[i]-r[i]);
         if(far>p[i-])
         {
             puts("-1");
             return ;
         }
     }
     printf("%lld\n",(p[n]-p[])*3ll);
     return ;
 }

Code