HDU2196computer

就是求每个点为起始点的最长链的长度。

写一下各个数组的意思吧。

f[i][0]为点i向下走最长的距离；f[i][1]为点i向下走第二长的距离；

xia[i][0]为点i向下走最长距离所要走的儿子节点；

xia[i][1]为点i向下走第二长长距离所要走的儿子节点；

f[i][2]为点i向上走的最大距离；

显而易见求向下的DP递推就好了。

求向上的DP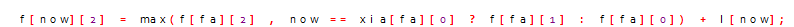

注意：两个DP都是从根节点往下更新。

#include<cstdio>
#include<algorithm>
#include<cstring>
#define maxn 10010 << 1
using namespace std;
int head[maxn],tot,n,u,v,val,len[maxn],f[maxn][];
int xia[maxn][],l[maxn];
struct st{
    int v,val,next;
    st clear(){
        v = val = next = ;
    }
}s[maxn];

void add(int u,int v,int val)
{
    tot++;
    s[tot].v = v;
    s[tot].val = val;
    s[tot].next = head[u];
    head[u] = tot;
}

void dfs(int fa,int now)
{
    for(int i=head[now];i;i=s[i].next)
        if(s[i].v != fa)
        {
            l[s[i].v] = s[i].val;
            dfs(now,s[i].v);
            len[now] = max(len[s[i].v] + s[i].val,len[now]);
            int k = len[s[i].v] + s[i].val;
            if(f[now][] < k)
            {
                f[now][] = k;
                xia[now][] = s[i].v;
            }
            if(f[now][] > f[now][])
            {
                swap(xia[now][],xia[now][]);
                swap(f[now][],f[now][]);
            }
        }
}

void find(int fa,int now)
{
    f[now][] = max(f[fa][] , now == xia[fa][] ? f[fa][] : f[fa][]) + l[now];
    for(int i=head[now];i;i=s[i].next)
        if(s[i].v != fa)
            find(now,s[i].v);
}

int main(){

    while(scanf("%d",&n) != EOF)
    {

        for(int i=;i<= * n;i++)
        {
            head[i] = f[i][] = f[i][] = f[i][] = len[i] = l[i] = xia[i][] = xia[i][] = ;
            s[i].clear();
        }
        tot = ;
        for(int i=;i<=n;i++)
        {
            scanf("%d%d",&v,&val);
            add(i,v,val);
            add(v,i,val);
        }

        dfs(,);

        find(,);

        for(int i=;i<=n;i++) printf("%d\n",max(f[i][],f[i][]));

    }
}