2-sat基础详解

（大量引用《2-SAT解法浅析 -by 华中师大一附中 赵爽》《由对称性解2-SAT问题》

Great_Influence关于P4782 【模板】2-SAT 问题的题解。在此对原作者表示衷心的感谢）

在实际的题目中，限制往往还有除了或以外的别的形式，这些限制也将在这篇文章中讨论。

先讨论以下两类限制的情况：

　　1、若x=a，则y=b

　　2、x=a或y=b

　　由于x、y都是bool变量，值要么1，要么0，所以可以通过建有向图的方式来表示这个题目。对每个bool变量x，都建立两个点，分别表示x=1和x=0。为了方便，以后的x表示图中的一个点（除非x前加“变量”两字，表示变量），~x表示点x的对应点（即另一个表示同一变量的点）。图中有了点，就要考虑边了。

　　设X_a （字母大写以区分上文小写字母表示内容）为变量x等于一个数a对应的点。同时下文的‘^’表示异或符号。显然对上面的两类限制都可以通过连边实现：

　　　　对于第一种限制，要增这样两条边：（X_a，Y_b）即变量x=a可推出变量y=b；（Y_(b^1),X_(a^1)）即变量y不等于b可推出变量x不等于a。

　　　　对于第二种限制，就要增这样两条边：（X_(a^1)，Y_b）即变量x不等于a可推出变量y等于b；（Y_(b^1),X_a）即变量y不等于b可推出变量x不等于a。

　　发现这些边都是对称的，即若连了一条边（x，y），则必会有边（~y，~x）（注意这里的字母是小写的）在同一时间连上。同时也发现这些边的意义也很好理解，不就是“推出”嘛。并且每种限制所连的两条边都很好地将这个限制表示了出来。那么有了一个最基本的解决问题的暴力算法了：从每个变量x开始，若它有标记，则直接看下一个变量，否则枚举它选1或选0，设选了b，并从相应的点dfs。在dfs过程中标记遍历过的变量都选什么（对正向边则标记为该边的终点；反向边则标记为该边的对应点。是的，这个dfs也要走反向边，即一切有关系的都要走）。若发现dfs过程中遍历了一组对应点，即从当前变量x选b可推出某个变量既选1又选0，这显然是矛盾的，故当前变量不能选b，要选另一个。若当前变量选1或0都不行，则无解了（这里用不用让之前的变量重新选一下，再重新枚举当前变量的取值呢？答案是不用。因为若当前变量要取枚举取1取0，则当前变量肯定与之前变量关系。因为有关系的都被打上标记了。所以之前变量的取值情况是与当前变量独立的）；否则就看下一个变量：    直到看完所有变量的值后发现仍没有矛盾，则每个变量枚举的值就是答案；或发现无解情况，就记录无解信息后停止就好。

　　显然这个算法是很慢的，时间复杂度可达O(n*m)。除非要求一个字典序最小的取值方案，否则一般都不用这个算法。下面介绍一个更快的算法：

　　我们考虑图的一个强连通分量。很明显，如果我们选中强连通分量中的任何一点，那么该强连通分量中的所有其它的顶点也必须被选择。所以我们可以先求图的所有强联通分量。当我们发现若一组对应点x和~x都在同一个强连通分量时，即若变量x选1，可推出它应该选0；它选0，可推出它应该选1，这样的话变量x不管怎么选都是矛盾的，则该2-sat无解。若没有这样的情况，那么我就叫他“前置合法”了，即已经满足了有解的前提之一。前置合法后，设原图为G，缩点后的图为G'，然后，我们把G'中的所有弧反向，得到图G′′。由于已经进行了缩点的操作，因此G′′中一定不存在圈，也就是说，G''具有拓扑结构。我们把G中所有顶点置为“未着色”。按照拓扑顺序重复下面的操作：

　　　1、选择第一个未着色的顶点u。把u染成红色。

　　　2、把所有与u矛盾的顶点（如果存在x,~x∈，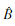

前置合法时，k=1建的边不会影响强连通分量的对称性。（因为这条边的起点与终点不会在同一个强联通分量里）。

证明正确性前先了解几个定理：

　　1、

　　2、

　　3、

下面证明一下该算法的正确性：

　　一、

　　二、

　　　　

　　　　1、

　　　　　　个人认为《2-SAT解法浅析》中有关二、1的证明是不正确的，这里可以举出一个反例：

　　　　　　　　

　　　　　　所以下文给出作者个人的关于二、1的证明：

　　　　

　　　　2、

　

故该算法是正确的。时间复杂度为O（n）（tarjan为O(n)，拓扑排序为O(n)，染色为O(n)（染色要注意不染重复的点，否则就可能变成O(n的平方)）。故总复杂度也为O(n)（实际上，更准确的说，这里的n为n*2））

其实还有一个常数的优化：

　　　　

　　故前置合法时必有解

故前置合法时，每个变量选他对应点中拓补序大的点，一定会得到一组解。这样的话就不用求完拓补序后再染色了。

再仔细考虑一下，发现tarjan的缩点的顺序正是一个反的拓补序，所以可以记录他tarjan的顺序，这样连拓扑序也不用求了。

代码