luogu P1038借教室【Noip提高组2012】

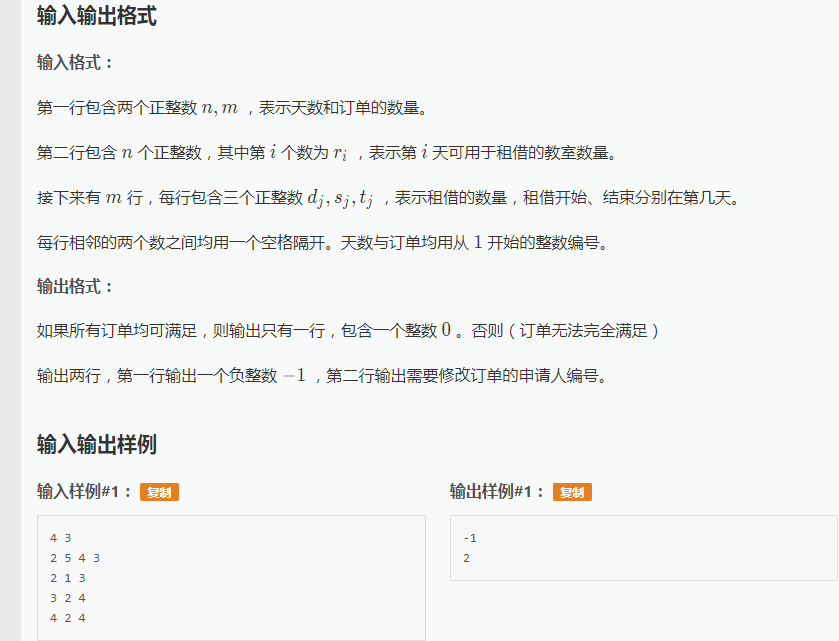
这道题我读完题目的第一感觉是：

这不就是个线段树？？用线段树维护区间最小值，检查是否满足订单要求即可判断。

对于修改操作直接在区间上进行。

据说会卡一卡线段树，但是貌似写一个懒标记，连zkw线段树都不用，然后读优，什么的随便卡卡就可以A了

后来想了想，就这么显然的直接拿线段树去A题显然没什么意义，于是决定想一波正解

正解的一般解法都是差分前缀和+二分

当然主要都是二分。

然后我绞尽脑汁不知道怎么写，后来发现是不会算复杂度限制了我的想象力。

二分天数十分显然，在1~m间二分，对于每一个mid,我们假定，订单就一定会在这一天出锅，然后剩下的就是判断这一天会不会出锅。

对于判断的方式，我们另开一个数组，记录类似订单能够为总的教室数量贡献或是拿走的信息

我们假设这个数组是room_add，order_l, order_r, order_room分别代表订单从第order_l天开始到第order_r天结束，每天借order_room间教室

对于每份订单：在room_add[order_l[i]]上加上order_room, 相应的，在room_add[order_r[i]+1]上减去order_room

分别表示订单在order_l天得到了order_room间教室，而在order_r天失去了order_room间教室，也就是为下一个订单提供了order_room间教室。

我们很容易想到，对于两份相邻的订单，若是后一份订单得到的教室加上前一份订单失去的教室的数量比a[i]（a[i]表示每天能提供的教室数量）还大，说明我们肯定无法满足后一份订单，就出锅了。

但是我们二分的是在哪一天出锅，所以这个时候我们要把二分范围缩小

反之扩大

最后如果二分结束后r等于m，就表示中间一定有出过锅，导致r的范围缩小了

详细见代码实现

 #include<bits/stdc++.h>
 #define ll long long
 #define uint unsigned int
 using namespace std;
 const int maxn = ;
 struct shiki {
     int l, r;
     int room;
 }order[maxn];
 int n, m;
 int a[maxn], room_add[maxn];

 inline int read() {
     int x = , y = ;
     char ch = getchar();
     while(!isdigit(ch)) {
         if(ch == '-') y = -;
         ch = getchar();
     }
     while(isdigit(ch)) {
         x = (x << ) + (x << ) + ch - '';
         ch = getchar();
     }
     return x * y;
 }

 inline bool check(int aim_day) {
     memset(room_add, , sizeof(room_add));
     for(register uint i = ; i <= aim_day; ++i) {
         room_add[order[i].l] += order[i].room;
         room_add[order[i].r + ] -= order[i].room;
     }
     for(register uint i = ; i <= n; ++i) {
         room_add[i] += room_add[i - ];
         if(room_add[i] > a[i]) return true;
     }
     return false;
 }

 int main() {
     n = read(), m = read();
     for(int i = ; i <= n; ++i)
          a[i] = read();
     for(int i = ; i <= m; ++i)
         order[i].room = read(), order[i].l = read(), order[i].r = read();
     int l = , r = m;
     while(l < r) {
         int mid = l + r >> ;
         if(check(mid)) r = mid;
         else l = mid + ;
     }
     if(r != m) cout << - << '\n' << l << '\n';
     else cout <<  << '\n';
     return ;
 }