RMQ总结

题目描述

给定N个数的序列和M次询问，每次询问给定左右端点区间中的最大值

输入样例:

6 (N)

34 1 8 123 3 2

4 (M)

1 2

1 5

3 4

2 3

输出样例:

34

123

123

8

题目分析

虽然是另一类问题，但分析方法实际采用的是类似区间dp的方法，具体定义见下图

需要说明的是，图中所说的长度是指元素的个数，而非元素之间的间隔数。例如序列1，2，3，长度为3。其实这里无论选择元素个数还是间隔数都能解题，保证后续的下标计算对应上即可。



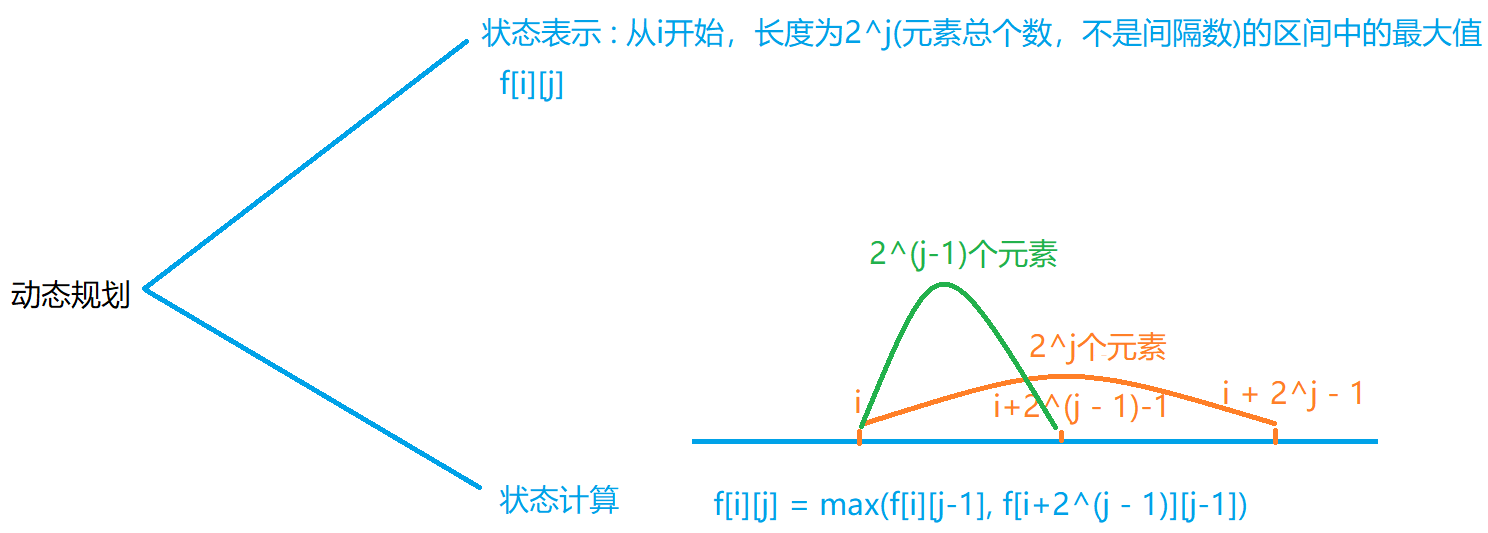
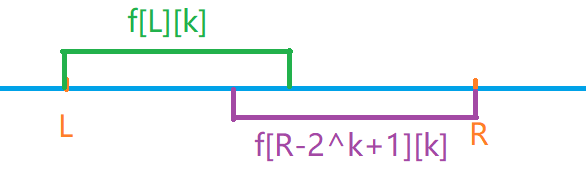
在上述初始化完成之后，对于一组询问，计算方法见下图。

很值得记忆的一点是当我们求解最值时，重合的区间并不会影响最终答案，我们只需保证所选区间能够覆盖整个区间即可。

下图中k的含义:满足 \(2^k <= len(R - L + 1)成立的最大值\)，显然\(2^k * 2 > len\)，假设不成立，那么当前的k就不是合法的k。所以我们选择的两个长度为\(2^k\)的区间一定是存在交集的，但是重复的数据对求解最大值并无影响，所以我们只需要在左右区间中找出最大值即可。

代码实现

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 2e5 + 10, M = 20;

int n, m;
int a[N];
int f[N][M];

void init()
{
    /**
     * 从转移方程可以看出，如果选择先预处理i，在更新f[i][j]时需要使用f[i + (2^j)][j - 1],显然是无法更新的
     * 但是如果选择先预处理j，在更新f[i][j]时候所需要的f[][j-1]都已经更新完全了，是可以正常更新的
     */
    for (int j = 0; j < M; ++ j) // 其实序列最长为200000，2^17 = 131072, 2^18 = 262144
        for (int i = 1; i + (1 << j) - 1 <= n; ++ i)
            if (!j) f[i][j] = a[i]; // 注意j=0时候对应长度为2^0=1，不是长度为0
            else f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}
int query(int l, int r)
{
    int len = r - l + 1;
    int k = log(len) / log(2); // log()求的是以10为底的对数

    return max(f[l][k], f[r- (1 << k) + 1][k]);
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> a[i];

    init();

    cin >> m;
    while (m --)
    {
        int l, r;
        cin >> l >> r;
        cout << query(l ,r) << endl;
    }

    return 0;
}