plicp 点云迭代最近邻点配准法

输入参数

• 点云A的极坐标集合
• 点云A对应Lidar所在pose
• 点云B的极坐标集合
• 点云B对应Lidar所在pose

Features

• 根据两个点云的弧度关系确定找点的起始位置
• 根据两个点云的弧度关系设置找点的停止条件
• 算出被投影点云的大跳小跳表，根据大跳小跳表来遍历点云

大跳小跳表(假设点云A中间点为a点)

建立大跳小跳表的前提点云的弧度是递增的

理论上来说当点云A的所有点的弧度都一样，那么点云A中长度和b点长度相同的点，距离最近

a点一共有两个大跳表和两个小跳表：

序号比a点小的点	序号比a点小的点		序号比a点大的点	序号比a点大的点
小跳表1(有序)	大跳表1(有序)		小跳表2(有序)	大跳表2(有序)
长度比a短	长度比a长		长度比a短	长度比a长

前提

1. 输入参数点云的极坐标的弧度是有序的(这里的有序不是说弧度是递增或者递减，而是说点是Lidar顺时针或者逆时针扫了一圈出来
2. 不同弧度上的任意两点长度越接近，距离越近
3. A和C之间区取余角，Lsin(余角)是A点距离CC'这条线最近距离

步骤

1. 过滤原始数据的无效点
   
   a. 原始数据中长度为0(或者近似)的点标记为无效
   
   b. 原始数据中长度过长(超出Lidar扫描能里的点)标记为无效
   
   c. 使用滑窗(2cm)，每次滑窗内的点合并成一个点(x和y取平均值)
2. 找出点云A和点云B各自的最小弧度和最大弧度
3. 排序点云(原始数据的有序请看前提1)，排序结果为弧度递增
4. 转换两个点云各自的迪达尔坐标
5. 计算两个点云对应Lidar pose的差
6. 根据Lidar pose的差，将点云B投影到点云A为C，算出C的笛卡尔坐标
7. 建立点云A的大跳小跳表
8. 算出点云A每弧度的点数量NumA
9. 遍历点云C的每个点X
   
   a. 算出X的极坐标
   
   b. 算出X点弧度和点云A最小弧度的差值，然后乘以NumA，得到的结果cur_idx是遍历点云A的起始点序号
   
   c. 如果保存了X的前一点在点云A最近点的序号last_beat_idx，那么X点就从last_beat_idx+1开始在点云A上找最近点，cur_idx=last_beat_idx+1
   
   d. 从X点的分别向前向后查找最近点，每次遍历都保存目前找到的最近距离dist(根据大跳小跳表遍历)
   
   e. 算出点云A任意一点a和X的弧度差raX，然后用X的长度做斜边，算出和X点弧度相差raX的点的距离best_dist(最近距离)，一旦之前存在dist <= best_dist，那么就认为找到了最近点D
10. 找到最近点D之后，算出点D前一个点D1和后一个点D2分别距离点X的距离，距离更短的点就认为是距离点X第二最近的点

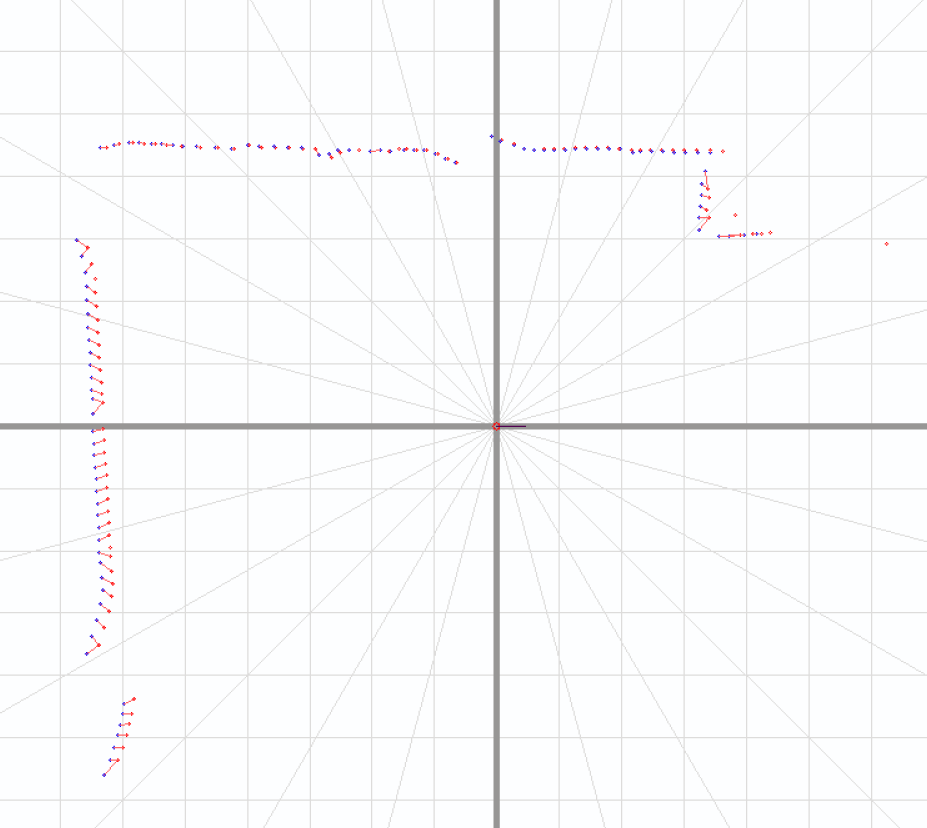
未完

一对多