李超树学习笔记 & JZOJ 5039. 【NOI2017模拟4.2】查询题解

李超树

它本质上是线段树的拓展运用

解决的问题：平面直角坐标系中，支持插入线段，问 \(x = x_0\) 这条直线上最大的 \(y\) 值

它维护的东西很奇特：优势线段

何为“优势线段”？

给定两条线在指定区间内，所有 \(x\) 对应的两个 \(y\) 高的数量越多的就是优势线段

如下

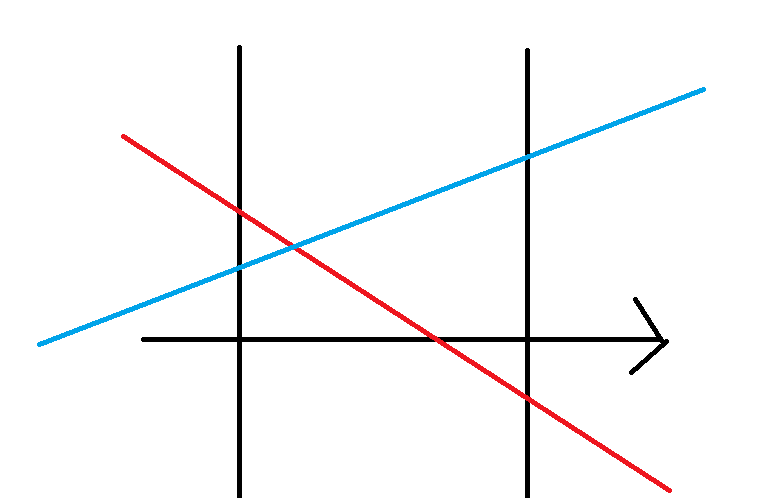
蓝线便是优势线段

我们在线段树对应的本区间就维护蓝线的斜率和截距就行了

不过红线不能就此抛弃，而应让它下放到它可能具有优势的区间

这样的话，我们需要把询问所在的区间跑完才能弄出答案

因为正确答案可能已经被下放到了比较靠下的地方，即更小的区间

以上是大致思路，具体过程如下

1. 此刻区间里面还没有维护的东西，那么直接更新线段树信息即可
2. 新线段与此刻线段树维护的线段没有交点，如果新线段在线段树维护的线段树之上，那么直接更新，否则 \(return\)
3. 新线段与此刻线段树维护的线段有交点，那么就需要分类讨论了。

当交点的 \(x\) 轴坐标在区间正中心的左侧时，如果新线段的斜率高于原线段，那么很明显线段树维护的值就要变成新线段了（上面的图就是这种情况），但在变成新线段之前要把原线段的信息下放到左子树（即交点所在的半个原区间）。若斜率低于原线段，那么本区间的优势线段没有变，就直接递归讨论线段树的左儿子即可。右侧同理，具体见例题代码。

最好自己手划一下，然后打一遍标程，再对一遍标程就会板了

时间复杂度：插入直线时，每次将直线的定义域分隔到 \(\log n\) 个区间，每个区间最多把标记下传 \(\log n\) 层，因此修改的时间复杂度为 \(\log(n^2)\)。（但常数不大）

总的复杂度是：\(nlog(n^2)\)

例题：

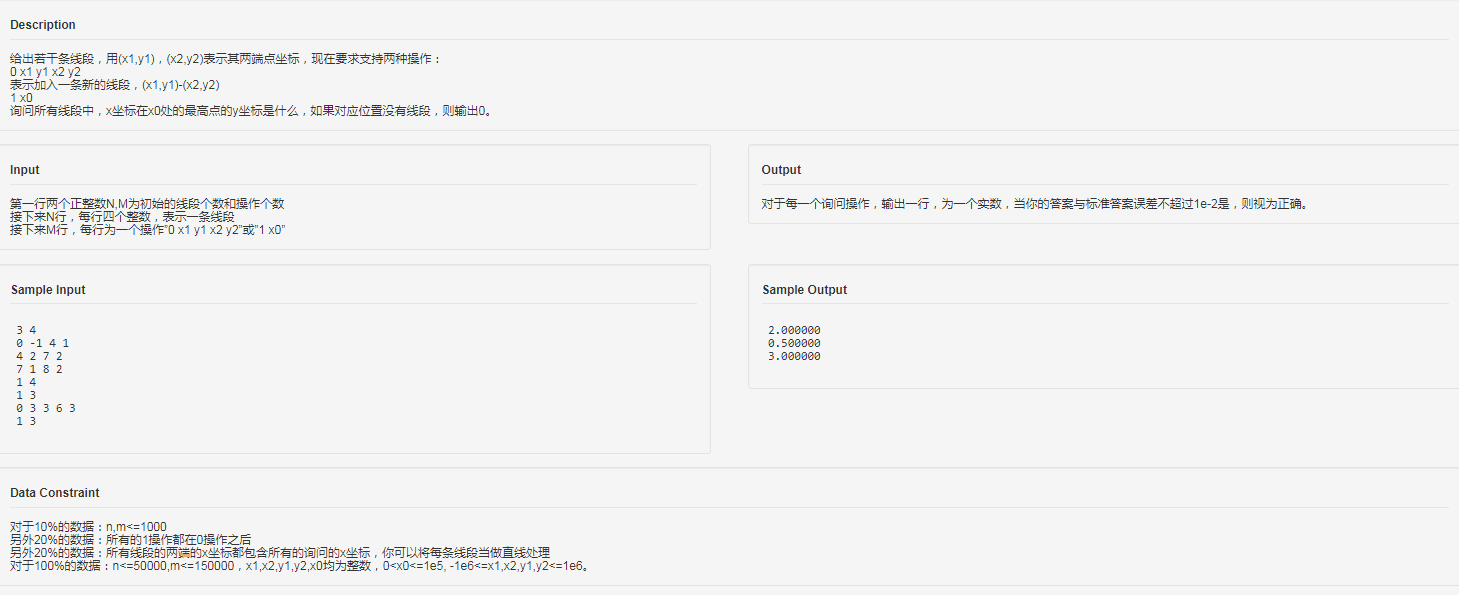
思路分析：裸题，直接上李超树

注意：加的是线段！即区间加入一条线段而非直线

而题中只需维护 \([1..10^5]\) 中线段的信息就行了

板子

\(Code\)

#include<cstdio>
using namespace std;

const int N = 1e5 + 5;
int n , m , fl[4 * N];

struct tree{
	long double k , b;
}seg[4 * N];

inline void swap(int &x , int &y){int t = x; x = y , y = t;}
inline long double max(long double x , long double y){return x < y ? y : x;}
inline long double min(long double x , long double y){return x < y ? x : y;}
inline long double Intersection(long double k1 , long double b1 , long double k2 , long double b2){return 1.0 * (b2 - b1) / (k1 - k2);}

inline void update(long double k , long double b , int x , int y , int l , int r , int rt)
{
	if (y < l || x > r) return;
	int mid = (l + r) >> 1;
	if (l >= x && r <= y)
	{
		if (!fl[rt])
		{
			seg[rt].b = b , seg[rt].k = k , fl[rt] = 1;
			return;
		}
		long double f1 = seg[rt].k * l + seg[rt].b , f2 = seg[rt].k * r + seg[rt].b;
		long double f3 = k * l + b , f4 = k * r + b;
		if (f1 >= f3 && f2 >= f4) return;
		else if (f1 <= f3 && f2 <= f4) seg[rt].k = k , seg[rt].b = b;
		else{
			long double len = Intersection(k , b , seg[rt].k , seg[rt].b);
			if (f1 <= f3)
			{
				if (len <= mid) update(k , b , x , y , l , mid , rt << 1);
				else update(seg[rt].k , seg[rt].b , x , y , mid + 1 , r , rt << 1 | 1) , seg[rt].k = k , seg[rt].b = b;
			}
			else{
				if (len > mid) update(k , b , x , y , mid + 1 , r , rt << 1 | 1);
				else update(seg[rt].k , seg[rt].b , x , y , l , mid , rt << 1) , seg[rt].k = k , seg[rt].b = b;
			}
		}
		return;
	}
	if (x <= mid) update(k , b , x , y , l , mid , rt << 1);
	if (y > mid) update(k , b , x , y , mid + 1 , r , rt << 1 | 1);
}

inline long double query(int l , int r , int rt , int x)
{
	long double ans = 1.0 * x * seg[rt].k + seg[rt].b;
	if (l == r) return ans;
	int mid = (l + r) >> 1;
	if (x <= mid) ans = max(ans , query(l , mid , rt << 1 , x));
	else ans = max(ans , query(mid + 1 , r , rt << 1 | 1 , x));
	return ans;
}

int main()
{
	freopen("query.in" , "r" , stdin);
	freopen("query.out" , "w" , stdout);
	scanf("%d%d" , &n , &m);
	int x1 , x2 , y1 , y2;
	long double k , b;
	for(register int i = 1; i <= 4 * 1e5 + 1; i++) seg[i].b = -1e18 , seg[i].k = 0;
	for(register int i = 1; i <= n; i++)
	{
		scanf("%d%d%d%d" , &x1 , &y1 , &x2 , &y2);
		if (x1 > x2) swap(x1 , x2) , swap(y1 , y2);
		if (x1 == x2) k = 0 , b = max(1.0 * y1 , 1.0 * y2);
		else k = 1.0 * (y1 - y2) / (x1 - x2) , b = 1.0 * y1 - 1.0 * k * x1;
		update(k , b , x1 , x2 , 1 , 1e5 , 1);
	}
	int opt;
	while(m--)
	{
		scanf("%d" , &opt);
		if (opt == 0)
		{
			scanf("%d%d%d%d" , &x1 , &y1 , &x2 , &y2);
			if (x1 > x2) swap(x1 , x2) , swap(y1 , y2);
			if (x1 == x2) k = 0 , b = max(1.0 * y1 , 1.0 * y2);
			else k = 1.0 * (y1 - y2) / (x1 - x2) , b = 1.0 * y1 - 1.0 * k * x1;
			update(k , b , x1 , x2 , 1 , 1e5 , 1);
		}
		else{
			scanf("%d" , &opt);
			long double ans = query(1 , 1e5 , 1 , opt);
			printf("%.6Lf\n" , ans == -1e18 ? ans = 0 : ans);
		}
	}
}