多校 HDU 6397 Character Encoding (容斥)

　　题意：在0~n-1个数里选m个数和为k，数字可以重复选；

　　　　如果是在m个xi>0的情况下就相当于是将k个球分割成m块，那么很明显就是隔板法插空，不能为0的条件限制下一共k-1个位置可以选择插入隔板，那么也就是说一共有C(k-1, m-1)种组合（m-1是因为要m块只要m-1个隔板）；

　　回到这题，我们要求的并不是m个xi>0、而是xi>=0，但是隔板之间又不能为空，最少也是1，那就让m块每块都有一个球就好了，这样最少为1个的隔板间也就相当于是0个；但是此时的隔板插空处就又增加了，那么此时就变为将m+k个球分割成m块的问题，一共k+m-1个空，也就是组合数量为C(k+m-1, m-1);

　　这样我们就知道了在xi无限制的情况下的组合数量，但是xi很明显是有限制的，对于xi有0<=xi<n；假设有m块里有1个xi>=n的情况下，要让问题保持在xi是取自[0, n-1]的范围内，那么就让那m块里其中一块变成已经放了n个球的情况，那么我们就相当于求在k-n+m-1个位置里插上m-1个隔板的方案数C(k-1*n+m-1, m-1)；但是这个一块有m个位置可以选，也就是包括刚刚插空的方案还要加上选择时的方案即一共C(m, 1)*C(k-1*n+m-1, m-1)；然后我们枚举当C(m, i)的i位为0~m时的所有情况， 令(-1)^i为容斥系数。答案就是

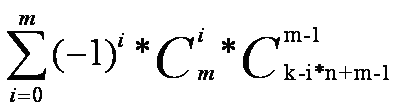
下面给出代码加注释：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int N=2e5+, INF=0x3f3f3f3f, mod=;///在这里k+m在最大值是2e5所以说保存阶乘和阶乘逆的数组要开2e5
 void ex_gcd(ll a, ll b, ll &d, ll &x, ll &y){
     if (!b) {d = a, x = , y = ;}
     else{
         ex_gcd(b, a % b, d, y, x);
         y -= x * (a / b);
     }
 }
 ll Inv(ll a, ll p){
     ll d, x, y;
     ex_gcd(a, p, d, x, y);
     return d ==  ? (x % p + p) % p : -;
 }
 ll inv[N]={, };///保存i!的逆元
 ll sum[N]={, };///保存i!
 ll getC(int n, int m){///得到C(n, m)
     if(n<m||m<){///如果不满足这些的情况是根本没有方案数的
         return ;
     }
     return ((sum[n]*inv[m])%mod)*inv[n-m]%mod;
 }
 int main( ){
     register int i, n, m, k, T;
     register ll l, ans;
     for(l=; l<N; ++l){
         sum[l]=(sum[l-]*l)%mod;
         inv[l]=Inv(sum[l], mod);
     }
     scanf("%d", &T);
     while(T--){
         ans=;
         scanf("%d%d%d", &n, &m, &k);
         for(i=; i*n<=k; ++i){
             if(i&){
                 ans=((ans-getC(m, i)*getC(k-i*n+m-, m-)%mod)%mod+mod)%mod;///斥
             }else{
                 ans=(ans+getC(m, i)*getC(k-i*n+m-, m-)%mod)%mod;///容
             }
         }
         printf("%lld\n", ans);
     }
 }

拙略的代码