你可以参考下面方法，进行动态为网页引用外部的Javascript脚本文件。代码写在Page_Init方法内。

VB.NET: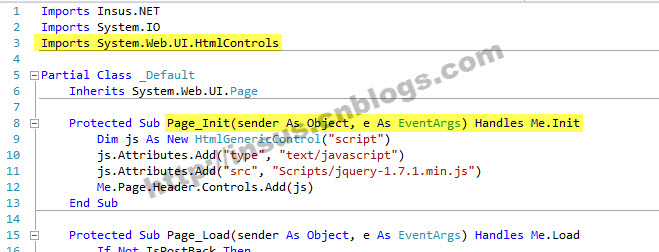

下图是运行时，查看HTML的源代码：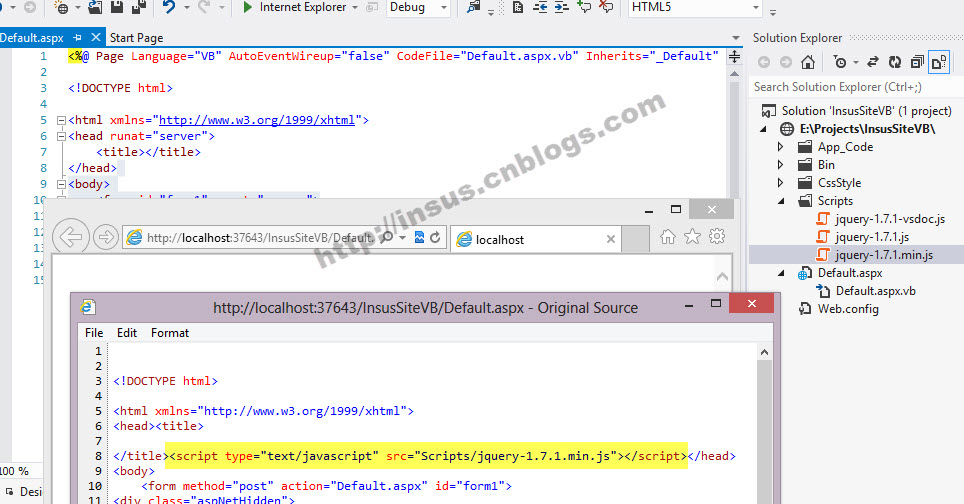

C#: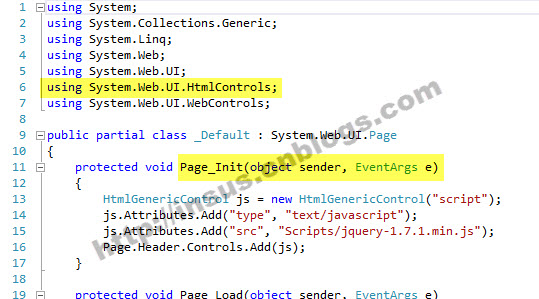

动态引用外部的Javascript脚本文件[转]的更多相关文章

  1. 获取当前正在执行的Javascript脚本文件的路径

    获取当前JavaScript脚本文件的路径,在特定场景下可能需要,比如写模块加载器,或者进行日志记录.下面这段脚本适用于所有浏览器来获取正在执行js文件的路径,但是该方法只适用于脚本加载过程中执行的情 ...

  2. Shell中 调用/引用/包含 另外的脚本文件的两种方法

    脚本 first (测试示例1) #!/bin/bash echo 'your are in first file' 问)在当前脚本文件中调用另外一个脚本文件? 方法一: 使用 source 脚本 s ...

  3. 动态装载外部JavaScript脚本文件

    当我们请求一个URL地址时,浏览器会从远程服务器装载各种所需的资源,如JavaScript.CSS.图片等.而在加载JavaScript时,常常会发生下面这种情况: 也就是说,当浏览器碰到Script ...

  4. ASP.NET中母版页引用外部js或css文件无效,提示对象未定义解决方法

    最近做网站用了一个js+css实现的带有二级菜单的导航条,在母版页创建好后,子页面调用出现了许多奇怪的问题,多方查证后的最终解决方案和大家分享下.... 1.路径问题 如果是一个单独的aspx页面调用 ...

  5. 如何使用 Chrome 浏览器调试动态加载的 Javascript 脚本

    在IE中,可以在调试程序的文档列表最下方看到一个"动态脚本"的文件夹,里面可以找到动态加载的脚本,但是...数量繁多,也不能自定义名称... 但是在 Chrome 中,貌似根本找不 ...

  6. 引用外部静态库(.a文件）时或打包.a时，Category方法无法调用。崩溃

    我的这个是MJRefresh,学习打.a包Terminating app due to uncaught exception 'NSInvalidArgumentException', reason: ...

  7. iOS 引用外部静态库(.a文件）时或打包.a时，Category方法无法调用。崩溃

    我的这个是MJRefresh,学习打.a包Terminating app due to uncaught exception 'NSInvalidArgumentException', reason: ...

  8. HTML中引用外部JS文件失效原因

    今天在练习中碰到“引用外部的一个js文件但是却失效”的情况,实在不懂,百度后才知是引用的位置不对,错误的代码如下: <head> <meta charset="UTF-8& ...

  9. 浏览器环境下JavaScript脚本加载与执行探析之代码执行顺序

    本文主要基于向HTML页面引入JavaScript的几种方式,分析HTML中JavaScript脚本的执行顺序问题 1. 关于JavaScript脚本执行的阻塞性 JavaScript在浏览器中被解析 ...

随机推荐

  1. Oracle中SYS_CONNECT_BY_PATH函数的妙用 ;

    Oracle 中SYS_CONNECT_BY_PATH函数是非常重要的函数,下面就为您介绍一个使用SYS_CONNECT_BY_PATH函数的例子,实例如下: 数据准备: ),b )); ', 'A' ...

  2. redis哨兵机制一(转)

    概述 Redis-Sentinel是Redis官方推荐的高可用性(HA)解决方案,当用Redis做Master-slave的高可用方案时,假如 master宕机了,Redis本身(包括它的很多客户端) ...

  3. [转帖]go 命令

    golang笔记——命令  https://www.cnblogs.com/tianyajuanke/p/5196436.html 1.GO命令一览 GO提供了很多命令,包括打包.格式化代码.文档生成 ...

  4. crosses initialization of “XXX” 的问题

    在switch-case中定义了变量,用g++编译的时候报错crosses initialization of “XXX” ,在网上一查,说是gcc要求变量的定义不能位于goto之后 将变量定义放在s ...

  5. Spring Boot 推荐的 Java 配置

    在学 Spring 的过程中 , 配置文件慢慢的被注解所替代 , 现在 Spring Boot 更是推荐使用 Java 配置完全来代替配置文件 . 需要使用到的注解有 : Bean 相关 : @Con ...

  6. Redis：主从复制

    前言 在前面的两篇文章中,分别介绍了Redis的内存模型和Redis的持久化. 在Redis的持久化中曾提到,Redis高可用的方案包括持久化.主从复制(及读写分离).哨兵和集群.其中持久化侧重解决的 ...

  7. 题解 CF1005A 【Tanya and Stairways】

    楼上别说这个题水,这个题可能还真有不知道的知识点. 看到这个题,想到刚学的单调栈. 单调栈? 单调栈和单调队列差不多,但是我们只用到它的栈顶. 单调,意思就是一直递增或者递减. 这跟这个题有什么关系? ...

  8. 怎么解决Xing欲

    怎么解决Xing欲 来源:微信号 王路在隐身 这是知乎上的一道问题.原题叫<和尚怎么解决性欲>. 本来由出家人回答更合适,但估计出家人一般不太愿意回答. 我看了几十个答案,几乎都是在调侃出 ...

  9. 【UOJ228】基础数据结构练习题（线段树）

    [UOJ228]基础数据结构练习题(线段树) 题面 UOJ 题解 我们来看看怎么开根? 如果区间所有值都相等怎么办? 显然可以直接开根 如果\(max-sqrt(max)=min-sqrt(min)\ ...

  10. 洛谷 P1306 斐波那契公约数 解题报告

    P1306 斐波那契公约数 题意:求\(Fibonacci\)数列第\(n\)项和第\(m\)项的最大公约数的最后8位. 数据范围:\(1<=n,m<=10^9\) 一些很有趣的性质 引理 ...