python中的递归问题，求圆周率

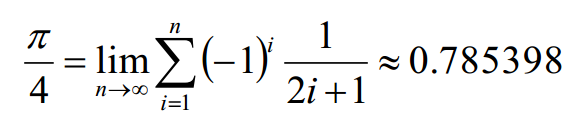
以上面一个公式为例：

import numpy as np
def getPi(n):
    if n == 0:
        return np.power(-1,n)*(1.0/(2*n+1))
    else:
        return np.power(-1,n)*(1.0/(2*n+1))+getPi(n-1)

print 4*getPi(100)

　　

可以通过上面一个递归实现。

参考

特点：

①递归就是在过程或者函数里调用自身。

②在使用递归策略时，必须有一个明确的递归条件，称为递归出口。

③递归算法解题通常显得很简洁，但递归算法解题的效率较低。所以一般不倡导使用递归算法设计程序。

④在递归调用的过程当中系统的每一层的返回点、局部变量等开辟了栈来存储。递归函数次数过多容易造成栈溢出等。

所以一般不倡导用递归算法设计程序。

要求：

递归算法所体现的"重复"一般有三个条件：

①每次在调用规模上都有所缩小（通常是减半）。

②相邻两次重复之间有紧密的联系，前一次要为后一次做准备（通常前一次的输出就作为后一次的输入）。

③在问题的规模极小时必须用直接接触解答而不再进行递归调用，因而每次递归调用都是有条件的（以规模未达到直接解答的大小为条件），

无条件的递归调用将会成为死循环而不能正常结束。

每当你调用一个函数，在这个函数执行前都会将之前的代码地址（也就是调用点）入栈，等被调用的函数执行完将地址出栈，程序根据这个数据返回调用点。
若递归调用次数太多，就会只入栈不出栈，于是堆栈就被压爆了，此为栈溢出。

python中的解决办法：

1、人为设置递归深度

import sys
sys.setrecursionlimit(1000000) #括号中的值为递归深度

　　事实上并不能完全解决，太多还是会程序崩溃的。

2、所谓的尾递归

import numpy as np

def getPi(n,m):
    if n == 0:
        return m+np.power(-1,n)*(1.0/(2*n+1))
    else:
        return getPi(n-1,m+np.power(-1,n)*(1.0/(2*n+1)))

print 4*getPi(100,0)

　　尾递归参考:https://www.cnblogs.com/hello--the-world/archive/2012/07/19/2599003.html

尾递归的写法就是将操作的值作为参数传递，事实上，python并不支持尾递归的优化！而且对递归的次数有限制，当递归深度超过1000时，会抛出异常。

故对于继续研究突破递归次数的话，虽然有高手找到解决办法，并没有太大意义。

3、利用迭代的方式，而不是使用递归（譬如，reduce）

import numpy as np

s = reduce(lambda x,n:x+np.power(-1,n)*(1.0/(2*n+1)),[np.power(-1,0)*(1.0/(2*0+1))]+range(1,100000))
print 4*s

s = reduce(lambda x,n:x+np.power(-1,n)*(1.0/(2*n+1)) if x>0 else np.power(-1,x)*(1.0/(2*x+1))+np.power(-1,n)*(1.0/(2*n+1)),\
          range(0,100000))
print 4*s

　　可以看到，利用reduce函数是处理这类问题的比较好的办法。用一句话总结：

                                                  普通程序员用迭代，天才程序员用递归！