AI数学基础之:P、NP、NPC问题

目录

• 简介
• P问题
• NP问题
  • NP问题的例子
  • 有些NP问题很难解决
• NPC问题
• NP-hard
• P和NP问题

简介

我们在做组合优化的时候需要去解决各种问题，根据问题的复杂度不同可以分为P、NP、NPC问题等。今天给大家来介绍一下这些问题类型。

P问题

在计算复杂度理论中，P（也称为PTIME或DTIME）是基本的复杂度类型。 它是指能够使用确定图灵机在多项式时间内解决的所有决策问题。

这里我们给一下P的定义，如果一个公式语言L是一个P类型，那么当且仅当存在这样的一个确定图灵机M时成立：

1. 对于所有的输入，M都会在多项式时间内运行
2. 对于L中所有的x, M的输出都是1
3. 对于不在L中的所有x，M输出都是0

常见的P问题包括线性规划的决策版本，计算最大公因数和找到最大匹配。 在2002年，证明了确定数字是否为质数的问题也是一个P问题。

NP问题

在计算复杂度理论中，NP（nondeterministic polynomial time）不确定性多项式时间主要用来衡量分类决策问题的复杂度。 NP是一组决策问题，对于这些问题实例来说，如果答案为“是”，那么表示该实例使用确定图灵机可在多项式时间内验证成功。

NP实际上是由两个阶段组成的，第一阶段包括对解决方案的猜测，该阶段以非确定性方式生成，而第二阶段包括确定性算法，验证猜测是否可以解决问题。也就是说NP= nondeterministic + polynomial。

根据P和NP的定义，我们可以发现所有的P问题都是NP问题，因为P的定义是所有问题都可以在多项式时间内确定地解决，而NP的定义是问题可以在多项式时间内得到验证的问题。

但是NP包含了更多的问题，其中NP中最难的问题被称为NP-complete 问题。解决多项式时间中的此类问题的算法也能够解决多项式时间中的任何其他NP问题。

NP问题的例子

在计算机科学中，很多搜索优化的问题都可以被看做是NP问题。旅行商问题就是一个典型的NP问题。

“给出一个城市列表以及每对城市之间的距离，要找到一条访问每个城市一次最后返回原城市的最短路径” 这是组合优化中的一个NP难题，在理论计算机科学和运筹学中很重要。

有些NP问题很难解决

因为NP问题中包含了很多实际生活中非常重要的问题，所以人们为查找NP中的多项式时间算法付出了巨大的努力。但是，NP中仍然存在许多问题，这些问题好像无法在多项式时间内得到解决。关于这些问题在多项式时间内是否能够被解决是计算机科学中最大的未解决问题之一。

在这种情况下，引入了一个重要的概念就是NP完全决策问题集(NP-complete),它是NP的子集，可以非正式地描述为NP中“最难”的问题。如果我们说一个问题被证明是NPC问题，那么意味着在这个问题上无法找到多项式时间算法。

但是，在实际应用中，通常不会花费大量的计算去寻找一个最优解，但是可以在多项式时间内找到一个次优解，这对于实际应用就已经足够了。

NPC问题

在计算复杂度理论中，满足以下情况的问题是NPC问题：

1. 一个不确定的图灵机可以在多项式时间内求解。
2. 确定性的Turing机可以在较大的时间复杂度中进行求解（EXPTIME或者暴力搜索算法），并且可以在多项式时间内验证其解。
3. 它可以用来模拟任何其他具有相似可解性的问题（NP中的其他问题都可以在多项式时间内转换或者规约为该问题）。

根据规则3，因为NPC问题是NP问题的更加复杂的形式，如果你可以找到一个解决某个 NP-complete 问题的多项式算法，那么所有的 NP 问题都将可以很容易地解决。

举个例子，一个一元一次方程可以规约为求一个一元二次方程，只需要将二次型系数变为0即可。通过不断地规约，我们能得到复杂度更高但是应用范围更广的算法来代替复杂度虽低但是应用范围小的一类问题的算法。

尽管可以“快速”验证NPC问题的解决方案，但是没有已知的方法可以快速找到解决方案。即，随着问题的大小增长，使用任何当前已知的算法解决问题所需的时间迅速增加。

仍未发现用于计算NP完全问题的解决方案的方法，但是计算机科学家和程序员仍然经常遇到NP完全问题。 NP完全问题通常通过使用启发式方法和近似算法来解决。

NP-hard

在计算复杂性理论中，NP-hard是对一类问题的描述，这些问题“至少与NP中最难的问题一样难”。 NP-hard问题的一个简单例子是子集和问题。

如果一个已知的NPC问题能够规约到此问题，那么这个问题就叫做NP-hard问题。

所以NPC问题一定是NP-Hard问题，但并不是所有的NP-Hard问题都是NPC问题。

P和NP问题

P和NP问题是计算机科学中尚未解决的主要问题。它谈论的是如果一个问题可以快速的被验证，那么该问题是否可以被快速解决？

P是指该问题能够在多项式时间内找到解决方案，而NP是指如果找到候选的答案，则能够进行快速验证。

一般情况下大家都任务P ！= NP，也就是说虽然无法在多项式时间内解决，但答案可以在多项式时间内验证。

根据P和NP是否相同，我们分别作出P、NP、NPC和NP-Hard的关系图。

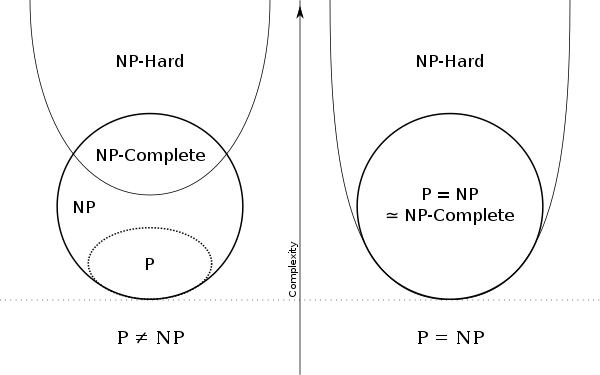
本文已收录于 http://www.flydean.com/04-p-np-npc-problem/

最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！

欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！