Log4j2再发新版本2.16.0,完全删除Message Lookups的支持,加固漏洞防御
昨天,Apache Log4j 团队再次发布了新版本:2.16.0!
2.16.0 更新内容
- 默认禁用JNDI的访问,用户需要通过配置log4j2.enableJndi参数开启
- 默认允许协议限制为:java、ldap、ldaps,并将ldap协议限制为仅可访问Java原始对象
- Message Lookups被完全移除,加固漏洞的防御
更多细节,可以通过官网查看:https://logging.apache.org/log4j/2.x/
如果您正在学习Spring Boot,那么推荐一个连载多年还在继续更新的免费教程:https://blog.didispace.com/spring-boot-learning-2x/
Spring Boot用户如何升级
Spring Boot用户依然可以通过前几天分享的Spring Boot应用简易升级Spring Boot下所有log4j版本的方法,去全局调整log4j2的版本。
如果你懒得看之前的文章,也可以通过下图了解具体如何修改:
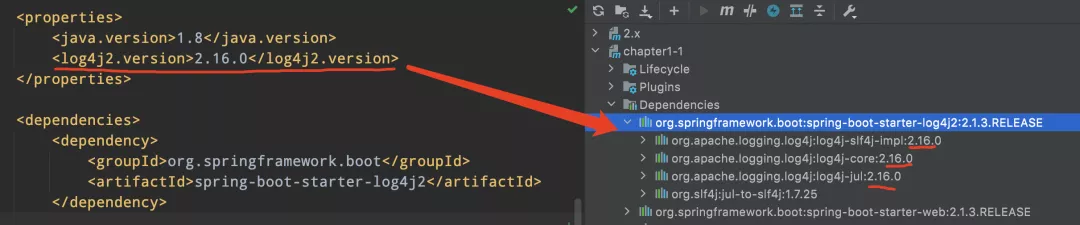
欢迎关注我的公众号:程序猿DD,分享外面看不到的干货与思考!
Log4j2再发新版本2.16.0,完全删除Message Lookups的支持,加固漏洞防御的更多相关文章
- 【紧急】继续折腾,Log4j再发2.1.6,强烈建议升级
背景 继前天正式发布的2.15.0之后,Apache log4j 2 团队宣布 Log4j 2.16.0 发布! 由于SLF4J适配兼容性的中断,Log4j 现在发布两个版本的SLF4J to Log ...
- Log4j2又爆雷!2.16.0存在DOS风险,升级2.17.0可解决
本以为,经过上周的2.16.0版本升级,Log4j2的漏洞修复工作,大家基本都要告一段落了. 万万没想到,就在周末,Log4j官方又发布了新版本:2.17.0 该版本主要修复安全漏洞:CVE-2021 ...
- 【紧急】Log4j又发新版2.17.0,只有彻底搞懂漏洞原因,才能以不变应万变,小白也能看懂
1 事件背景 经过一周时间的Log4j2 RCE事件的发酵,事情也变也越来越复杂和有趣,就连 Log4j 官方紧急发布了 2.15.0 版本之后没有过多久,又发声明说 2.15.0 版本也没有完全解决 ...
- CentOS 6.5 搭建 .NET 环境, Mono 5.16.0 + Jexus 5.8
最近有这样一个打算,就是准备把以前的有一个.NET 网站部署在Linux 下面,正好试试 .NET 跨平台的功能,为后续研究 .netCore 方向准备. 搭建环境: CentOS 6.5 + Mon ...
- linux下安装Nginx1.16.0
因为最近在倒腾linux,想安装新版本的nginx,找了一圈教程没有找到对应的教程,在稍微倒腾了一会之后终于成功的安装了最新版. 服务器环境为centos,接下来是详细步骤: 安装必要依赖插件 yum ...
- centos7编译安装LNMP(nginx-1.16.0,mysql8.0.16,php-7.3.6)常见问题报错及解决方法
LNMP的安装与配置 nginx-1.16.0安装及配置: 第一步:前往官网下载nignx源码包 下载完毕后上传至服务器(先安装lrzsz) yum -y install lrzsz 安装完毕后执行: ...
- 安装MYSQL详细教程 版本:mysql-installer-community-5.7.16.0 免安装版本和安装版本出现错误的解决
一.版本的选择 之前安装的Mysql,现在才来总结,好像有点晚,后台换系统了,现在从新装上Mysql,感觉好多坑,我是来踩坑,大家看到坑就别跳了,这样可以省点安装时间,这个折腾了两天,安装了好多个版本 ...
- 盘点 React 16.0 ~ 16.5 主要更新及其应用
目录 0. 生命周期函数的更新 1. 全新的 Content API 2. React Strict Mode 3. Portal 4. Refs 5. Fragment 6. 其他 7. 总结 生命 ...
- Greenplum5.16.0 安装教程
Greenplum5.16.0 安装教程 一.环境说明 1.1官方网站 Greenplum官方安装说明:https://gpdb.docs.pivotal.io/5160/install_guide/ ...
随机推荐
- 一个简单的golang项目,实验 gitlab-ci-cd Pipelines
至少两台主机,gitlab + gitlab-runner gitlab + gitlab-runner安装略 项目源码:https://gitee.com/M27149/testgo.git 在自建 ...
- [源码解析] PyTorch分布式(6) -------- DistributedDataParallel -- 初始化&store
[源码解析] PyTorch分布式(6) ---DistributedDataParallel -- 初始化&store 目录 [源码解析] PyTorch分布式(6) ---Distribu ...
- FastAPI 学习之路(六十一)使用mysql数据库替换sqlite数据库
我们首先需要安装对应的连接的依赖 pip install pymysql 然后在配置testDatabase.py from sqlalchemy import create_engine from ...
- PAT A1020——已知后序中序遍历求层序遍历
1020 Tree Traversals Suppose that all the keys in a binary tree are distinct positive integers. Give ...
- Water 2.4 发布,一站式服务治理平台
Water(水孕育万物...) Water 为项目开发.服务治理,提供一站式解决方案(可以理解为微服务架构支持套件).基于 Solon 框架开发,并支持完整的 Solon Cloud 规范:已在生产环 ...
- github文件下载加速器
https://d.serctl.com/?dl_start
- 解决FastJson中"$ref重复引用"的问题方法
对象的引用重复使用造成了重复引用问题,Fastjson默认开启引用检测将相同的对象写成引用的形式: 1 2 3 4 5 {"$ref": "$"} // 引用根 ...
- Codeforces 585E - Present for Vitalik the Philatelist(简单莫反+狄利克雷前缀和)
Codeforces 题目传送门 & 洛谷题目传送门 一道不算太难的 D1E 罢--虽然我不会做/kk u1s1 似乎这场 Div1 挺水的?F 就是个 AC 自动机板子还被评到了 3k2-- ...
- exit(0) exit(1) return() 3个的区别
exit(0):正常运行程序并退出程序: exit(1):非正常运行导致退出程序: return():返回函数,若在主函数中,则会退出函数并返回一值. 详细说: 1. return返回函数值,是关键字 ...
- 19.Happy Number-Leetcode
Write an algorithm to determine if a number is "happy". A happy number is a number defined ...
