嘻哈第二篇，深度聊聊各种细节.

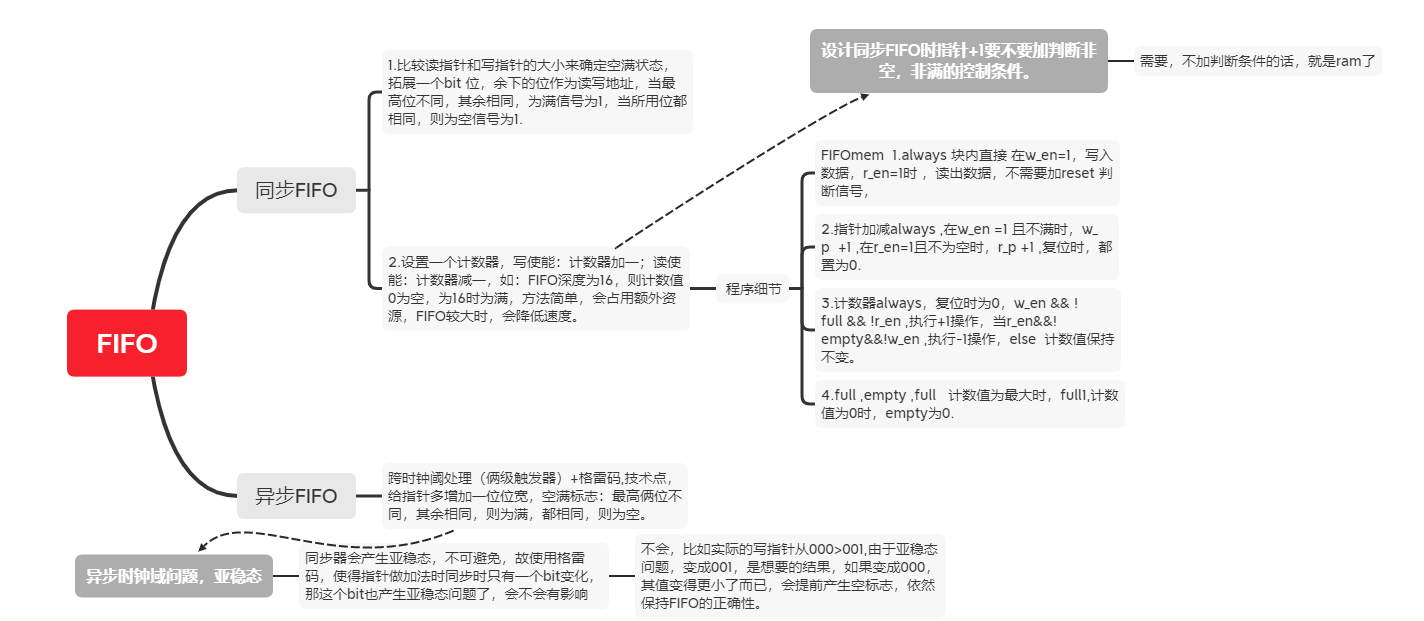
优化与跨时钟阈分析

FIFO 深度了解的更多相关文章

  1. 深入理解FIFO（包含有FIFO深度的解释）——转载

    深入理解FIFO(包含有FIFO深度的解释) FIFO: 一.先入先出队列(First Input First Output,FIFO)这是一种传统的按序执行方法,先进入的指令先完成并引退,跟着才执行 ...

  2. 深入理解FIFO（包含有FIFO深度的解释）

    FIFO: 一.先入先出队列(First Input First Output,FIFO)这是一种传统的按序执行方法,先进入的指令先完成并引退,跟着才执行第二条指令. 1．什么是FIFO? FIFO是 ...

  3. FIFO深度

    async fifo的full和empty的判断: 1)binary进制,MSB相同时,LSB也相同,empty: MSB不同时,LSB相同,full 2)gray code,MSB相同时,LSB也相 ...

  4. FIFO

    FIFO存储器 FIFO是英文First In First Out 的缩写,是一种先进先出的数据缓存器,他与普通存储器的区别是没有外部读写地址线,这样使用起来非常简单,但缺点就是只能顺序写入数据,顺序 ...

  5. 异步fifo的设计

    本文首先对异步 FIFO 设计的重点难点进行分析 最后给出详细代码 一.FIFO简单讲解 FIFO的本质是RAM, 先进先出 重要参数:fifo深度(简单来说就是需要存多少个数据)           ...

  6. 转：FIFO的定义与作用

    一.先入先出队列(First Input First Output,FIFO)这是一种传统的按序执行方法,先进入的指令先完成并引退,跟着才执行第二条指令. 1．什么是FIFO? FIFO是英文Firs ...

  7. Altera FIFO IP核时序说明

    ALTERA在LPM(library of parameterized mudules)库中提供了参数可配置的单时钟FIFO(SCFIFO)和双时钟FIFO(DCFIFO).FIFO主要应用在需要数据 ...

  8. FPGA FIFO深度计算

    转自:http://comm.chinaaet.com/adi/blogdetail/37555.html 首先,一定要理解清楚FIFO的应用场景,这个会直接关系到FIFO深度的计算,如果是面试官抛出 ...

  9. FIFO深度计算

    本文设计思想采用明德扬至简设计法.在使用FPGA设计系统时,常需要利用FIFO进行数据缓存保证数据不丢失,因此计算FIFO深度是至关重要的.FIFO的深度主要取决于“最恶劣”的情况,以下对于两种最常见 ...

随机推荐

  1. POJ 2065 SETI 高斯消元解线性同余方程

    题意: 给出mod的大小,以及一个不大于70长度的字符串.每个字符代表一个数字,且为矩阵的增广列.系数矩阵如下 1^0 * a0 + 1^1 * a1 + ... + 1^(n-1) * an-1 = ...

  2. POJ 2663 Tri Tiling dp 画图找规律

    状态:d[i]代表n=i时的方案数. 状态转移方程:d[i]=d[i-2]+2*(d[i-2]+d[i-4]+-+d[0]) i只会为偶数,奇数情况不存在,d[0]=1 找状态转移方程的时候画图更好理 ...

  3. Java：Java的堆区、栈区和方法区详解

    Java内存空间理解 堆:堆主要存放Java在运行过程中new出来的对象,凡是通过new生成的对象都存放在堆中,对于堆中的对象生命周期的管理由Java虚拟机的垃圾回收机制GC进行回收和统一管理.类的非 ...

  4. Mysql/Oracle/达梦中数据字典表

    在mysql中,数据字典表存放在information_schema库中,,对应的两张表,分别是TABLES,和COLUMNS. 在oracle中有表空间(即用户空间或者库)和模式的概念.模式和表空间 ...

  5. PHP解决并发问题的几种实现（转）

      对于商品抢购等并发场景下,可能会出现超卖的现象,这时就需要解决并发所带来的这些问题了 在PHP语言中并没有原生的提供并发的解决方案,因此就需要借助其他方式来实现并发控制. 方案一:使用文件锁排它锁 ...

  6. 计算机网络体系结构整理-第二单元IP技术

    IP技术 1.IPV4 Ipv4的报头格式 Ipv4地址分为ABCDE类, 类别 IP地址范围 私有IP地址范围 A 0.0.0.0-127.255.255.255 10.0.0.0-10.255.2 ...

  7. python对象类型

    一.内置对象 对象类型 分类 是否可变 例子 数字 数值 否 123,3.12 字符串 序列 否 'test',"test's" 列表 序列 是 [1,2,3,[1,2,'test ...

  8. 测试基础（四）Jmeter基础使用

    前言 通过测试基础(三) Jmeter安装 - 大风北吹 - 博客园 (cnblogs.com)安装完成Jmeter后,就可以使用Jmeter进行性能测试. 一.线程组 (1).线程组分类 Jmete ...

  9. JAVA基础之JDK、JRE、JVM关系

    什么是JRE和JDK JDK(Java Development Kit Java开发工具包) JDK是提供给Java开发人员使用的,其中包含了java的开发工具,也包括了JRE.所以安装了JDK,就不 ...

  10. Gradle入门第一集【下载，安装和测试】

    参考:https://www.cnblogs.com/panchanggui/p/9394760.html 1,http://services.gradle.org/distributions/链接下 ...