编译原理-DFA与正规式的转化
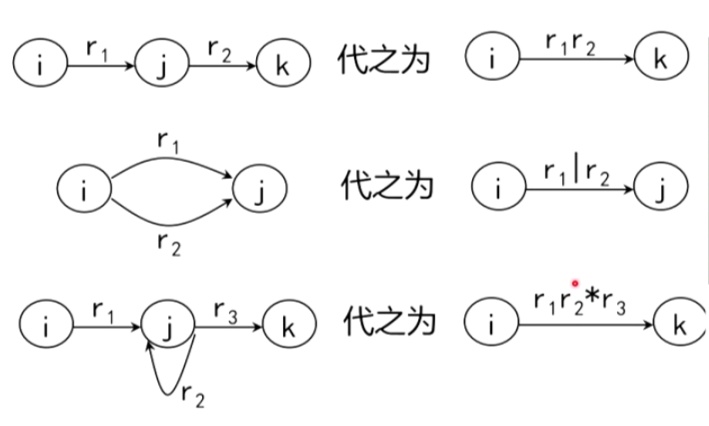
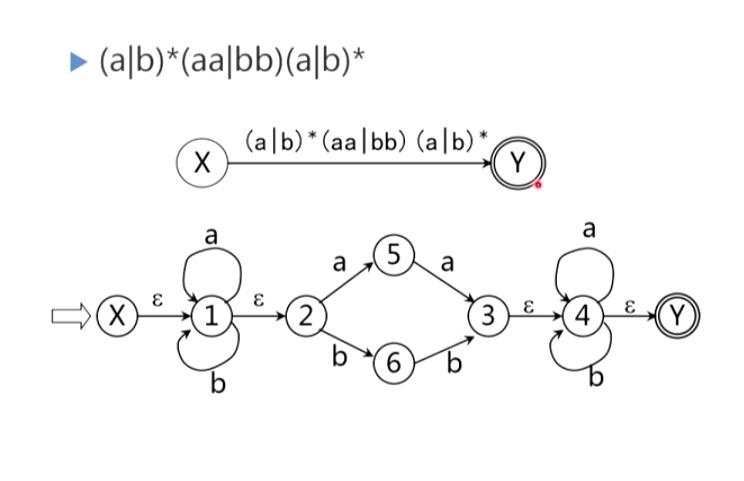
编译原理-DFA与正规式的转化的更多相关文章
- 正则表达式引擎的构建——基于编译原理DFA(龙书第三章)——3 计算4个函数
整个引擎代码在github上,地址为:https://github.com/sun2043430/RegularExpression_Engine.git nullable, firstpos, la ...
- 编译原理-DFA的化简(最小化)
对于给定的DFA M,寻找一个状态数比M小的DFA M'使得L(M)=L(M') 1.状态的等价性: 假设s和t为M的两个状态 ①若分别从状态s和状态t出发都能读出某个字α而停止于终态,则 ...
- 编译原理 DFA(确定性有穷自动机)&& NFA(非确定性有穷自动机)
https://www.cnblogs.com/fpcbk/p/11004913.html
- 《编译原理》构造与正规式 (0|1)*01 等价的 DFA - 例题解析
<编译原理>构造与正规式 (0|1)*01 等价的 DFA - 例题解析 解题步骤: NFA 状态转换图 子集法 DFA 的状态转换矩阵 DFA 的状态转图 解: 已给正规式:(0|1)* ...
- 编译原理:正规式转变成DFA算法
//将正规式转变成NFApackage hjzgg.formal_ceremony_to_dfa; import java.util.ArrayList; class Edge{ public int ...
- 编译原理课后习题答案令A,B和C是任意正规式,证明以下关系成立(A|B)*=(A*B*)*=(A*|B*)*
题目: 令A.B和C是任意正规式,证明以下关系成立: A∣A=A (A*)*= A* A*=ε∣A A* (AB)*A=A(BA)* (A∣B)*=(A*B ...
- 有穷自动机(NFA、DFA)&正规文法&正规式之间的相互转化构造方法
在编译原理(第三版清华大学出版社出版)中第三章的词法分析中,3.4.3.5.3.6小节中分别讲解了 1.什么是NFA(不确定的有穷自动机)和DFA(确定的有穷自动机) 2.如何将 不确定的有穷自动机 ...
- 编译原理-NFA构造DFA
本题摘自北邮的编译原理与技术. 首先,根据此图构造状态转换表 表中第一列第一行表示从第一个符号B通过任意个空转换能到达的节点,Ia表示由此行的状态数组({B,5,1}可以看作0状态)经过一个a可以到达 ...
- 【编译原理】c++实现自下而上语法分析及中间代码(四元式)生成
写在前面:本博客为本人原创,严禁任何形式的转载!本博客只允许放在博客园(.cnblogs.com),如果您在其他网站看到这篇博文,请通过下面这个唯一的合法链接转到原文! 本博客全网唯一合法URL:ht ...
随机推荐
- PKI/CA与证书服务
目录 PKI CA RA LDAP目录服务 CRL证书作废系统 数字证书 证书验证 证书撤销 证书更新 PKI系统的构成 PKI PKI(Public Key Infrastructure)公钥基础设 ...
- Swift系列五 - 可选项
可选项,一般也叫可选类型,它允许将值设为nil. 一.定义可选项 平时开发中,如果我们需要把一个变量置空时只需要把变量赋值一个nil即可: 上面尝试后不行,那怎么把一个变量置空呢? 答案:把变量设置可 ...
- Tars-Java客户端源码分析
一.基本RPC框架简介 在分布式计算中,远程过程调用(Remote Procedure Call,缩写 RPC)允许运行于一台计算机的程序调用另一个地址空间计算机的程序,就像调用本地程序一样,无需额外 ...
- 《前端运维》一、Linux基础--基础命令(1)
在开始之前,你需要做一些准备工作,去阿里买一台服务器,服务器的具体细节其实并不是十分重要,我也不会在这里一步一步的教大家如何去买一个服务器.百度一下足够了,但是还是要贴一下这篇文章中,我所使用的服务器 ...
- angularjs中的常遇问题整理
1.页面中默认图片的显示 {{img || "/upload/img.png"}} 2.接口中的数据没有及时读取到,$apply $.post( url, {}, function ...
- php单列模式和工厂模式
一.单例模式又称为职责模式,它用来在程序中创建一个单一功能的访问点,通俗地说就是实例化出来的对象是唯一的.所有的单例模式至少拥有以下三种公共元素: 1. 它们必须拥有一个构造函数,并且必须被标记为pr ...
- Spring Cloud Gateway + Nacos(1)简单配置
当初我学习时候就是参考这位大佬的博客: Nacos集成Spring Cloud Gateway 基础使用 现在学习到spring cloud alibaba 使用nacos做服务中心,dubbo做通信 ...
- IP子网划分与聚合
一:IP地址: IP地址是由32位2进制数组成,每8位一组.由点分十进制表达. IP地址可以分为五类 A类(1.0.0.0-126.255.255.255),127.0.0.1 为本地回环地址. B类 ...
- BUAA OS实验调试指南:从看懂到看开
一般的调试流程其实很简单:发现问题,稳定复现,确定临界条件,定位问题,修复问题,核查结果.迭代这个过程,形成一个闭环 老实说,OS的实验代码,开箱体验极差,程序跳来跳去,进了Lab4后还要考虑内核态切 ...
- traefik ingress Controller使用
Kubernetes Ingress Kubernetes Ingress是路由规则的集合,这些规则控制外部用户如何访问Kubernetes集群中运行的服务. 在Kubernetes中,有三种方式可以 ...
