QML插件扩展（一）

准备分两节来介绍QML扩展插件，分别为

（一）基于QML文件的扩展方式

（二）基于C++的插件扩展

这篇先介绍基于QML的插件扩展。

先介绍几个基本概念：

qmldir: 用于组织自定义的QML插件，qmldir的具体写法可参考

.qmltypes：qml插件的解释文件，用于QtCreator语法高亮。可通过Qt提供的工具qmlplugindump自动生成

QML_IMPORT_PATH: 导入插件路径，以支持插件的语法高亮。个人理解是如果纯QML文件的扩展，没有封装到C++中，则直接导入路径，即可支持语法高亮，如果有C++封装，则需要通过.qmltypes支持高亮。

addImportPath: 添加import寻址目录，c++代码里添加，没有前两项，只是QtCreator不能高亮，没有这种，则插件无法使用。

具体步骤

一、建立插件工程

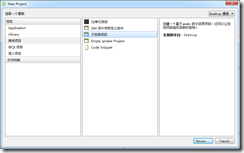
1.建立工程，首先通过QtCreator创建一个QMLPluginTest子目录工程：

2.在QMLPluginTest子目录下，添加app测试工程

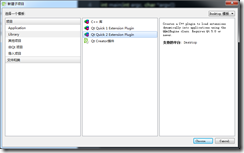
3.新建QML插件工程，MyPlugin

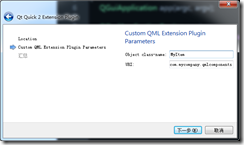
4.新建向导会自动创建示例文件及插件名称，这里可自己修改URI名称，即你的插件名称

5.自动创建的MyPlugin生成目录结构如图：

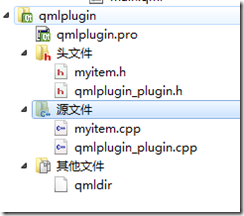
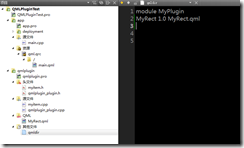
其中qmldir文件描述的插件的组成：

module MyPlugin

   plugin QMLPlugin

6.这节只介绍纯QML的插件方式，先不管自动生成的插件文件。

7.在MyPlugin目录下，添加扩展qml，这里添加一个测试矩形，MyRect.qml

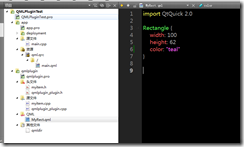
8.在qmldir中添加MyRect.qml,

二、使用插件

1. 在app工程的main.qml中，import MyPlugin 1.0,

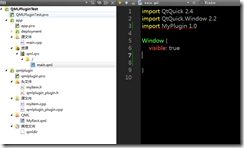
2.主要到右边代码中有让人郁闷的波浪线，说明QtCreator没有识别你的插件，需要QML_IMPORT_PATH来标记，打开app.pro文件

默认创建时QML_IMPORT_PATH =，没有赋值，修改为插件的路径，建议这里使用相对路径

QML_IMPORT_PATH = $$PWD/../

3.关闭QtCreator，重新打开,可以红色波浪线么有了

4.在main.qml中，使用创建的MyRect

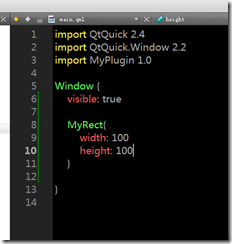
5.最后一步，导入插件路径，在app的main.cpp添加import代码，如果没有这句，程序启动会报错误：

qrc:/main.qml:3 module "MyPlugin" is not installed

所以需在c++中添加importPath，代码如下：

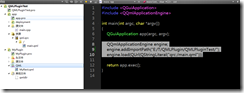
QQmlApplicationEngine engine;

engine.addImportPath("E:/T/QMLPlugin/QMLPluginTest/");(注意这里导入路径是MyPlugin的上层文件夹，不是MyPlugin文件夹）

如果没有指定插件的生成目录，在release或者debug模式下编译, 在release模式下生成的路径为"...\QMLPlugin\release"，需要新建一个MyPlugin

文件夹，把"...\QMLPlugin\release\QMLPlugin.dll"和”...\QMLPlugin\qmldir“一起拷贝到MyPlugin文件夹里面，然后将MyPlugin的上层文件夹

放到addImportPath（“”）中，比喻我的电脑为“E:\QT Project\TQ\LeiSigSlot\build-QMLPluginTest-Desktop_Qt_5_2_1_MinGW_32bit-Release\QMLPlugin”，插件目录为“E:\QT Project\TQ\LeiSigSlot\build-QMLPluginTest-Desktop_Qt_5_2_1_MinGW_32bit-Release\QMLPlugin\MyPlugin”

engine.load(QUrl(QStringLiteral("qrc:/main.qml")));

6.最后的程序目录结构：

附录：

1.程序生成路径：E:\T\QMLPlugin\build

2.程序源代码下载地址

https://github.com/youngerking1985/QML_Learn/tree/master/QMLPlugin1