JavaScript超大整数加法

原文:JavaScript超大整数加法

什么是「超大整数」？

JavaScript 采用 IEEE754标准 中的浮点数算法来表示数字 Number。

我也没花时间去详细了解 IEEE754标准 ，但对于处理超大整数，了解下面的几个知识点就足够了。

首先，JavaScript 实际上可以表示的最大数是: 1.7976931348623157e+308

Number.MAX_VALUE;    // 1.7976931348623157e+308

虽然这个数可以正确表示出来，但会存在「精度丢失」的问题。

那什么是「精度丢失」？ 我们看看下面的例子：

num1 = 10000000000000000000000000 + 11111111111111111111111111;    // 2.111111111111111e+25
num2 = 21111111111111111111111000;    // 2.111111111111111e+25
num1 === num2;    // true

按照常规的数学预算， num1 的计算结果是 21111111111111111111111111，而 num2 的值是 21111111111111111111111000，两者是不可能相等。但实际上 JavaScript 可以精确表示到个位的最大整数是：9007199254740992

Math.pow(2, 53);    //
Math.pow(2, 53) === Math.pow(2, 53) + 1;    // true
9007199254740992 === 9007199254740992 + 1;    // true

关于 JavaScript Number 的一些上下极限，更详细的资料可以看下图：

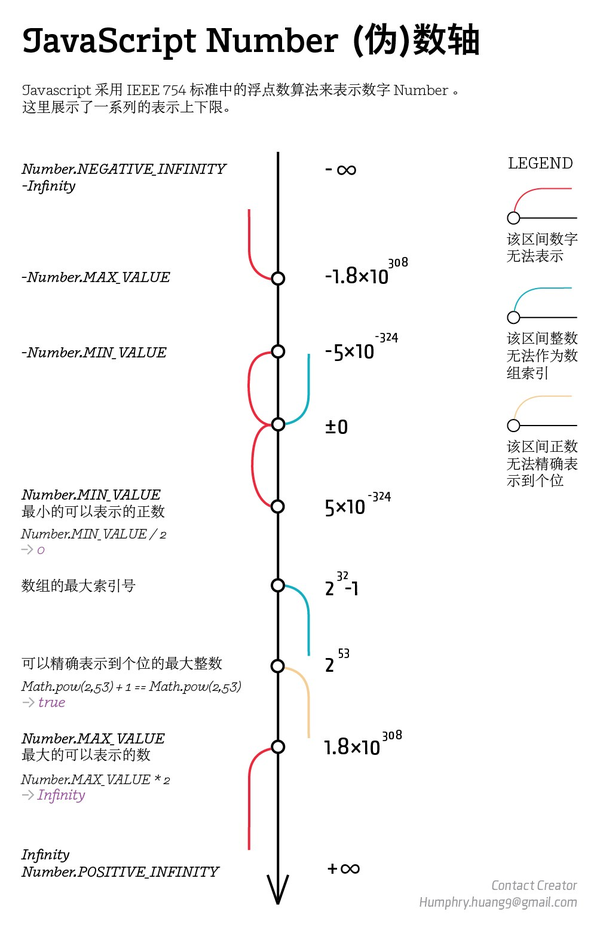
正因为 JavaScript 的 Number 类型存在这些限制，当我们需要处理两个「超大整数」的相加时，直接套用加法运算符会存在以下问题：

• 当结果大于 Math.pow(2, 53)  时，会出现精度丢失，导致最终结果存在偏差
• 当结果大于 Number.MAX_VALUE，直接返回 Infinity

为了解决这些问题，才产生了「超大整数」加法的需求，实现代码如下：

var largeIntegerAddition = function () {
    function isNumberString() {
        var result = true;
        for (var i = arguments.length; i--;) {
            if (typeof arguments[i] !== 'string' || !/^\d+$/.test(arguments[i])) {
                console.error('arguments format is incorrect!');
                result = false;
                break;
            }
        }
        return result;
    }

    function trimHeadZero(numberStr) {
        return numberStr.replace(/^0*/, '');
    }

    return function () {
        var bigNum1 = arguments[0],
            bigNum2 = arguments[1];

        if (!bigNum2) {
            return isNumberString(bigNum1) ? trimHeadZero(bigNum1) : '0';
        } else {
            if (!isNumberString(bigNum1, bigNum2)) {
                return '0';
            }

            bigNum1 = trimHeadZero(bigNum1);
            bigNum2 = trimHeadZero(bigNum2);

            var carry = 0,  // 进位
                bigNum1Split = bigNum1.split('').reverse(),
                bigNum2Split = bigNum2.split('').reverse(),
                result = '',
                maxNumSize = bigNum1Split.length > bigNum2Split.length ? bigNum1Split.length : bigNum2Split.length;

            for (var i = 0; i < maxNumSize; i++) {
                var n1 = bigNum1Split[i] ? +bigNum1Split[i] : 0,
                    n2 = bigNum2Split[i] ? +bigNum2Split[i] : 0,
                    sum = (n1 + n2 + carry).toString();
                if (sum.length > 1) {
                    carry = +sum.slice(0, 1);
                    result = sum.slice(1, 2) + result;
                } else {
                    carry = 0;
                    result = sum + result;
                }
            }

            if (carry !== 0) {
                result = carry + result;
            }

            if (arguments[2]) {
                var argumentArr = Array.prototype.slice.call(arguments, 0).slice(2);
                argumentArr.unshift(result);
                return largeIntegerAddition.apply(this, argumentArr);
            } else {
                return result;
            }
        }
    }
}();

测试用例：

// 测试用例
function unitTest(arg, result) {
    var res = largeIntegerAddition.apply(this, arg);
    console.log(res, res === result);
}
unitTest([], '');
unitTest(['012', 3], '15');
unitTest(['012', '0013', '214', 100002], '100241');
unitTest(['1.1111111111111111e+227', '1'], '1.1111111111111111e+227');
unitTest(['123'], '123');
unitTest(['1', '2', '3', '4', '5', '6', '7', '8', '9', '0'], '45');
unitTest(['0', '2', '3', '4', '123'], '132');
unitTest(['012', '3'], '15');
unitTest(['012', '0013', '214', '100002'], '100241');
unitTest(['99999999999999999999', '1'], '100000000000000000000');
unitTest(['99999999999999999999', '11111111111111111111'], '111111111111111111110');
unitTest(['99999999999999999999', '11111111111111111111', '11111111'], '111111111111122222221');
unitTest(['4810284728175829182', '92817475910285750182'], '97627760638461579364');
unitTest(['4810284728175829182', '92817475910285750182', '9728172845'], '97627760648189752209');
unitTest(['4810284728175829182', '92817475910285750182', '9728172845' , '92875018002020102'], '97720635666191772311');
unitTest([
    (function () {
        var str = '';
        for (var i = 500; i--;) {
            str += '9';
        }
        return str;
    })(),
    (function () {
        var str = '';
        for (var i = 500; i--;) {
            str += '1';
        }
        return str;
    })()
], (function () {
    var str = '';
    for (var i = 500; i--;) {
        str += '1';
    }
    return str + '0';
})());

本文作者：Maple Jan

本文链接：http://www.cnblogs.com/maplejan/p/3893545.html