luogu P1821 Silver Cow Party

题目描述

One cow from each of N farms (1 ≤ N ≤ 1000) conveniently numbered 1..N is going to attend the big cow party to be held at farm #X (1 ≤ X ≤ N). A total of M (1 ≤ M ≤ 100,000) unidirectional (one-way roads connects pairs of farms; road i requires Ti (1 ≤ Ti ≤ 100) units of time to traverse.

Each cow must walk to the party and, when the party is over, return to her farm. Each cow is lazy and thus picks an optimal route with the shortest time. A cow's return route might be different from her original route to the party since roads are one-way.

Of all the cows, what is the longest amount of time a cow must spend walking to the party and back?

寒假到了，N头牛都要去参加一场在编号为X（1≤X≤N）的牛的农场举行的派对（1≤N≤1000），农场之间有M（1≤M≤100000）条有向路，每条路长Ti（1≤Ti≤100）。

每头牛参加完派对后都必须回家，无论是去参加派对还是回家，每头牛都会选择最短路径，求这N头牛的最短路径（一个来回）中最长的一条路径长度。

输入输出格式

输入格式：

第一行三个整数N，M, X；

第二行到第M+1行：每行有三个整数Ai，Bi, Ti ,表示有一条从Ai农场到Bi农场的道路，长度为Ti。

输出格式：

一个整数，表示最长的最短路得长度。

输入输出样例

输入样例#1：

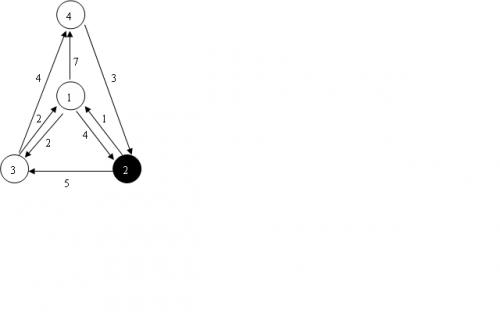
4 8 2
1 2 4
1 3 2
1 4 7
2 1 1
2 3 5
3 1 2
3 4 4
4 2 3

输出样例#1：

10

说明

可以算得上是最短路的比较模板的题目了。

首先理解一下题意，既然要算来回的路径距离，当然要求两遍最短路了，反正我是想不出更好的办法了。

来回的距离那自然不难想出，正着建边后，再反向建边。

我们需要在第一次建边的时候用数组将遍的两点记录下来，方便下次建边。

然后跑两遍最短路spfa就好啦。

代码：

/*
    Name: luogu 1821 Silver Cow Party
    Author: Manjusaka
    Date: 18-07-14 14:25
*/
 
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
using  namespace std;
#define N int(1e3+2)
#define M int(1e5+2)
int a[M],b[M],c[M];
int n,m,s,ans;
int head[N],tot;
struct ahah{
    int nxt,to,dis;
}edge[M];
int d[N],dd[N];
void add(int x,int y,int z)
{
    edge[++tot].nxt=head[x],edge[tot].to=y,edge[tot].dis=z,head[x]=tot;
}
bool vis[N];
queue <int> que;
void spfa(int s)
{
    for(int i=;i<=n;i++)d[i]=0x7fffff;
    vis[s]=;que.push(s);d[s]=;
    while(!que.empty())
    {
        int temp=que.front();
        vis[temp]=; que.pop();
        for(int i=head[temp];i;i=edge[i].nxt)
        {
            int v=edge[i].to;
            if(d[v]>d[temp]+edge[i].dis)
            {
                d[v]=d[temp]+edge[i].dis;
                if(!vis[v])
                {
                    vis[v]=;
                    que.push(v);
                }
            }
        }
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&s);
    for(int i=;i<=m;i++)
    {
        scanf("%d%d%d",&a[i],&b[i],&c[i]);
        add(a[i],b[i],c[i]);
    }
    spfa(s);
    for(int i=;i<=n;i++)dd[i]=d[i];
    tot=;
    memset(vis,,sizeof(vis));
    memset(head,,sizeof(head));
    for(int i=;i<=m;i++)add(b[i],a[i],c[i]);
    spfa(s);
    for(int i=;i<=n;i++)
    {
        if(d[i]+dd[i]>ans)ans=d[i]+dd[i];
    }
    printf("%d",ans);
}