NetworkX系列教程(10)-算法之三:关键路径问题

小书匠Graph图论

重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图论中常用算法弄个明白在写这部分.

图论常用算法看我的博客:

下面我将使用NetworkX实现上面的算法,建议不清楚的部分打开两篇博客对照理解.

我将图论的经典问题及常用算法的总结写在下面两篇博客中:

图论---问题篇

图论---算法篇

目录:

* 11.3关键路径算法(CPA)

---

注意:如果代码出现找不库,请返回第一个教程,把库文件导入.

11.3关键路径算法(CPA)

以下代码从这里复制,由于版本问题,将代码中的:nx.topological_sort(self, reverse=True)改为list(reversed(list(nx.topological_sort(self))))

1. import networkx as nx 
   

   ---

2. import matplotlib.pyplot as plt 
   

   ---

3. from matplotlib.font_manager import *  
   

   ---

4. ---

5. #定义自定义字体，文件名从1.b查看系统中文字体中来  
   

   ---

6. myfont = FontProperties(fname='/usr/share/fonts/truetype/wqy/wqy-zenhei.ttc')  
   

   ---

7. #解决负号'-'显示为方块的问题  
   

   ---

8. matplotlib.rcParams['axes.unicode_minus']=False  
   

   ---

9. ---

10. class CPM(nx.DiGraph): 
    

    ---

11. ---

12. def __init__(self): 
    

    ---

13. super().__init__() 
    

    ---

14. self._dirty = True 
    

    ---

15. self._critical_path_length = -1 
    

    ---

16. self._criticalPath = None 
    

    ---

17. ---

18. def add_node(self, *args, **kwargs): 
    

    ---

19. self._dirty = True 
    

    ---

20. super().add_node(*args, **kwargs) 
    

    ---

21. ---

22. def add_nodes_from(self, *args, **kwargs): 
    

    ---

23. self._dirty = True 
    

    ---

24. super().add_nodes_from(*args, **kwargs) 
    

    ---

25. ---

26. def add_edge(self, *args): # , **kwargs): 
    

    ---

27. self._dirty = True 
    

    ---

28. super().add_edge(*args) # , **kwargs) 
    

    ---

29. ---

30. def add_edges_from(self, *args, **kwargs): 
    

    ---

31. self._dirty = True 
    

    ---

32. super().add_edges_from(*args, **kwargs) 
    

    ---

33. ---

34. def remove_node(self, *args, **kwargs): 
    

    ---

35. self._dirty = True 
    

    ---

36. super().remove_node(*args, **kwargs) 
    

    ---

37. ---

38. def remove_nodes_from(self, *args, **kwargs): 
    

    ---

39. self._dirty = True 
    

    ---

40. super().remove_nodes_from(*args, **kwargs) 
    

    ---

41. ---

42. def remove_edge(self, *args): # , **kwargs): 
    

    ---

43. self._dirty = True 
    

    ---

44. super().remove_edge(*args) # , **kwargs) 
    

    ---

45. ---

46. def remove_edges_from(self, *args, **kwargs): 
    

    ---

47. self._dirty = True 
    

    ---

48. super().remove_edges_from(*args, **kwargs) 
    

    ---

49. ---

50. #根据前向拓扑排序算弧的最早发生时间 
    

    ---

51. def _forward(self): 
    

    ---

52. for n in nx.topological_sort(self): 
    

    ---

53. es = max([self.node[j]['EF'] for j in self.predecessors(n)], default=0) 
    

    ---

54. self.add_node(n, ES=es, EF=es + self.node[n]['duration']) 
    

    ---

55. ---

56. #根据前向拓扑排序算弧的最迟发生时间 
    

    ---

57. def _backward(self): 
    

    ---

58. #for n in nx.topological_sort(self, reverse=True): 
    

    ---

59. for n in list(reversed(list(nx.topological_sort(self)))): 
    

    ---

60. lf = min([self.node[j]['LS'] for j in self.successors(n)], default=self._critical_path_length) 
    

    ---

61. self.add_node(n, LS=lf - self.node[n]['duration'], LF=lf) 
    

    ---

62. ---

63. #最早发生时间=最迟发生时间,则判断该节点为关键路径上的关键活动 
    

    ---

64. def _compute_critical_path(self): 
    

    ---

65. graph = set() 
    

    ---

66. for n in self: 
    

    ---

67. if self.node[n]['EF'] == self.node[n]['LF']: 
    

    ---

68. graph.add(n) 
    

    ---

69. self._criticalPath = self.subgraph(graph) 
    

    ---

70. ---

71. @property 
    

    ---

72. def critical_path_length(self): 
    

    ---

73. if self._dirty: 
    

    ---

74. self._update() 
    

    ---

75. return self._critical_path_length 
    

    ---

76. ---

77. @property 
    

    ---

78. def critical_path(self): 
    

    ---

79. if self._dirty: 
    

    ---

80. self._update() 
    

    ---

81. return sorted(self._criticalPath, key=lambda x: self.node[x]['ES']) 
    

    ---

82. ---

83. def _update(self): 
    

    ---

84. self._forward() 
    

    ---

85. self._critical_path_length = max(nx.get_node_attributes(self, 'EF').values()) 
    

    ---

86. self._backward() 
    

    ---

87. self._compute_critical_path() 
    

    ---

88. self._dirty = False 
    

    ---

89. ---

90. if __name__ == "__main__": 
    

    ---

91. ---

92. #构建graph 
    

    ---

93. G = CPM() 
    

    ---

94. G.add_node('A', duration=5) 
    

    ---

95. G.add_node('B', duration=2) 
    

    ---

96. G.add_node('C', duration=4) 
    

    ---

97. G.add_node('D', duration=4) 
    

    ---

98. G.add_node('E', duration=3) 
    

    ---

99. G.add_node('F', duration=7) 
    

    ---

100. G.add_node('G', duration=4) 
     

     ---

101. ---

102. G.add_edges_from([ 
     

     ---

103. ('A', 'B'), 
     

     ---

104. ('A', 'C'), 
     

     ---

105. ('C','D'), 
     

     ---

106. ('C','E'), 
     

     ---

107. ('C','G'), 
     

     ---

108. ('B','D'), 
     

     ---

109. ('D','F'), 
     

     ---

110. ('E','F'), 
     

     ---

111. ('G','F'), 
     

     ---

112. ])  
     

     ---

113. ---

114. #显示graph 
     

     ---

115. nx.draw_spring(G,with_labels=True) 
     

     ---

116. plt.title('AOE网络',fontproperties=myfont) 
     

     ---

117. plt.axis('on') 
     

     ---

118. plt.xticks([]) 
     

     ---

119. plt.yticks([]) 
     

     ---

120. plt.show() 
     

     ---

121. ---

122. ---

123. print('关键活动为:') 
     

     ---

124. print(G.critical_path_length, G.critical_path) 
     

     ---

125. ---

126. G.add_node('D', duration=2) 
     

     ---

127. print('\n修改D活动持续时间4为2后的关键活动为:') 
     

     ---

128. print(G.critical_path_length, G.critical_path) 
     

     ---

关键路径示例(该图非黑色线为手工绘制,数字手工添加)

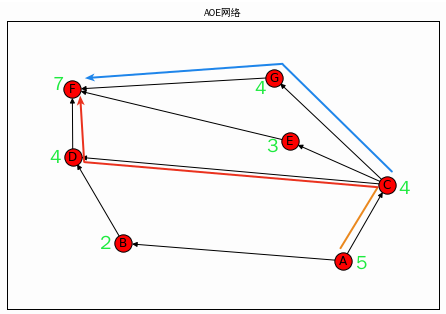
从graph中可以知道,有两条关键路径,分别是:A->C->G->F和A->C->D->F,长度都是20.

输出:

关键活动为: 20 ['A', 'C', 'D', 'G', 'F']

修改D活动持续时间4为2后的关键活动为: 20 ['A', 'C', 'G', 'F']

关键活动为: ['A', 'C', 'D', 'G', 'F'],可以构成两条边.D活动持续时间4为2后,关键路径变化.