SIGAI深度学习第一集 机器学习与数学基础知识

SIGAI深度学习课程：

本课程全面、系统、深入的讲解深度学习技术。包括深度学习算法的起源与发展历史，自动编码器，受限玻尔兹曼机，卷积神经网络，循环神经网络，生成对抗网络，深度强化学习，以及各种算法的应用。通过精心设计的实践项目，让你深刻理解算法的原理，真实学会算法的使用。

本讲：

讲授机器学习中的基本概念和算法、分类，以及微积分、线性代数、概率论、最优化方法等数学基础知识

机器学习简介：

特征向量

目标函数

机器学习分类：

有监督学习：分类问题（如人脸识别、字符识别、语音识别）、回归问题

无监督学习：聚类问题、数据降维

强化学习：根据当前状态预测下一个状态，回报最大化，回报具有延迟性，如无人驾驶、下围棋

深度学习数学知识：微积分、线性代数、概率论、最优化方法

一元函数微积分：

一元函数的泰勒展开：多项式近似代替函数

一定是在某一点附近做泰勒展开的

一元微分学：导数、泰勒展开、极值叛变法则。

多元函数微积分：

偏导数：其他变量当做常量，对其中一个变量求导数。

高阶偏导数：一般情况下，混合二阶偏导数与求导次序无关。

梯度：多元函数对各自变量的一阶偏导数构成的向量。

多元函数的泰勒展开

线性代数：

向量：n维空间的一个点。数学常为列向量，而在编程中常为行向量（按行优先存储）

向量的运算：加法、数乘、减法、内积、转置、向量的范数（将向量映射成一个非负的实数）

向量的范数：L-p范数分量绝对值的p次方求和再开p次方。L1范数：分量绝对值求和。L2范数：向量的长度/模。

矩阵：就是二维数组。矩阵的逆；矩阵的特征值；矩阵的二次型。

张量：相当于编程语言中的多维数组，n阶张量。

矩阵是2阶张量，向量是1阶张量。例如RGB彩色图像就是3阶张量。

雅克比矩阵：为所有因变量对所有自变量的偏导数构成的矩阵，雅克比矩阵的每一行为一个多元函数的梯度。

Hessian矩阵：多元函数的二阶偏导数构成的矩阵，是一个对称矩阵，相当于一元函数的二阶导数。

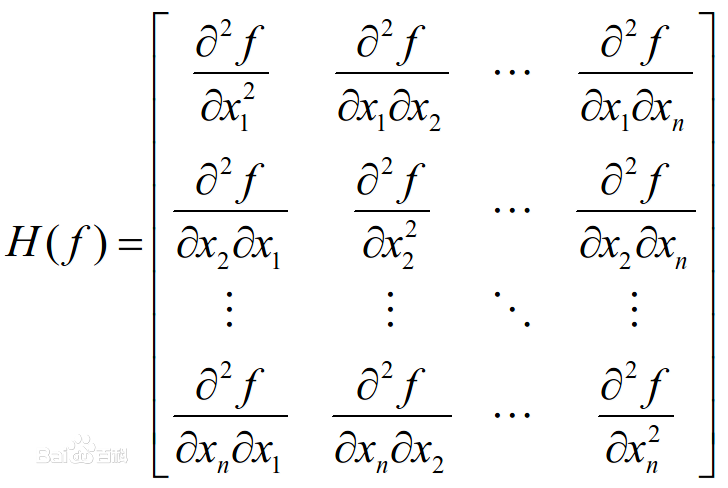
多元函数的极值判别法则：Hessian矩阵作用相当于f''(x)

如果Hessian矩阵正定，函数在该点有极小值；如果Hessian矩阵负定，函数在该点有极大值；如果Hessian矩阵不定，则为鞍点，不是极值点。

矩阵正定的定义：x[T]Ax>0

矩阵正定的判别法则：矩阵的特征值全大于0，矩阵的所有顺序主子式都大于0，矩阵合同于单位阵。

矩阵与向量求导：

wTx对x的梯度=w

xTAx对x的梯度=(A+AT)x

xTAx对x的Hessian算子（Hessian矩阵）=A+AT

概率论：

随机事件，随机事件的概率

条件概率：

p(a,b)=p(b|a)*p(a)     p(a,b)=p(a|b)*p(b)   =>p(b|a)*p(a)=p(a|b)*p(b)

贝叶斯公式:

将上式两边除以p(b)得到：p(a|b)=p(a)*p(b|a)/p(b)　　将a看做因，将b看做果，那么p(b|a)称为先验概率，p(a|b)称为后验概率，贝叶斯公式就是建立在先验概率和后验概率之间的关系。

随机事件的独立性p(a,b,c)=p(a)p(b)p(c)

随机变量：

随机事件量化后的一个变量，取每个值关联一个概率值的变量。

离散型随机变量：

取值只有有限种情况，或者无限种可列情况（如0到正无穷的所有整数为无限可列，而0到1的所有实数为无限不可列）。描述离散型随机变量的概率分布：p(x=xi)≥0，∑p(x=xi)=1.

连续型随机变量：

取值为无限不可列种情况，即一个区间内的实数。描述连续型随机变量的是概率密度函数和分布函数，概率密度函数要满足：f(x)≥0，∫f(x)dx=1；分布函数定义为F(y)=p(x≤y)=∫f(x)dx