nnUNet 论文解析
一些废话:
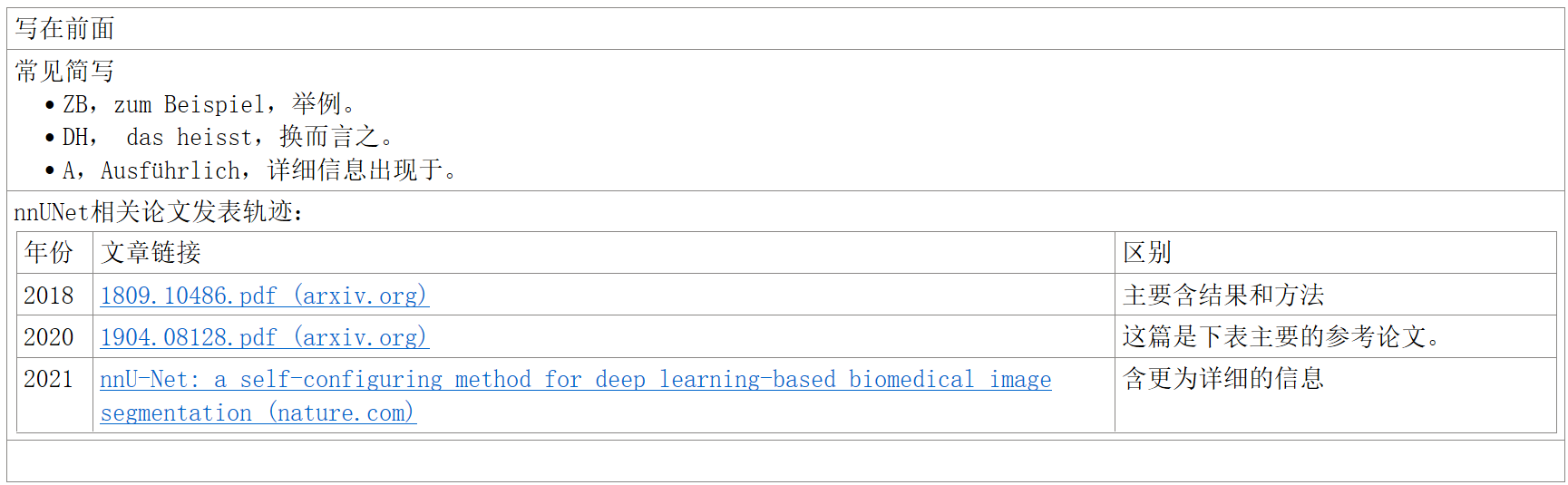
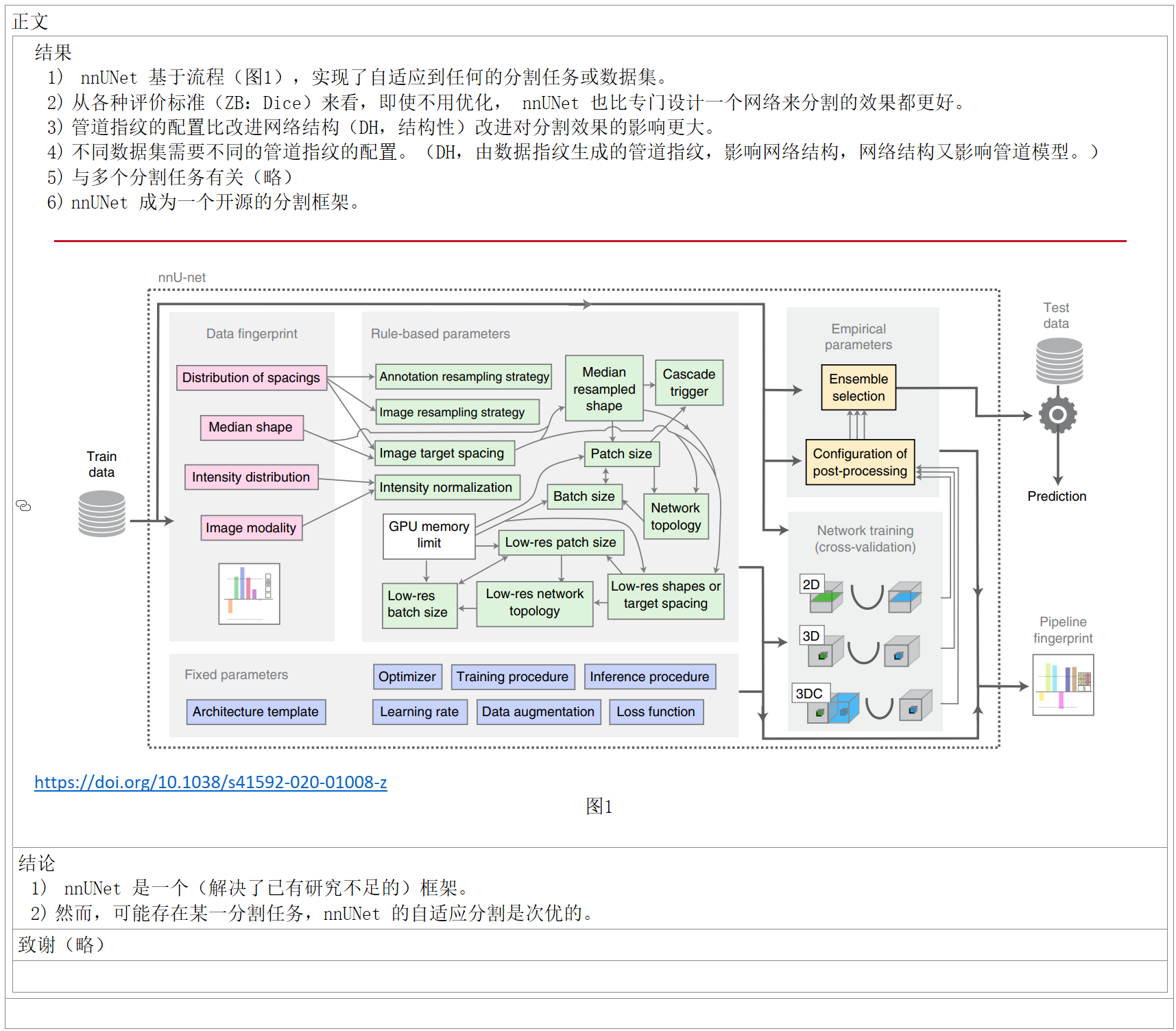
毕业论文用 nnUNet 及其自带的功能大概做了一个医学图像的分割模块。现将自己在学习过程中看过的相关论文及相关能找到的笔记记录整理在此。一些浅显的内容目的是在为自己做记录的同时,也希望能帮助到一些刚刚开始使用 nnUNet 的人。如有错处感谢指正。



nnUNet 论文解析的更多相关文章
- [Network Architecture]Mask R-CNN论文解析(转)
前言 最近有一个idea需要去验证,比较忙,看完Mask R-CNN论文了,最近会去研究Mask R-CNN的代码,论文解析转载网上的两篇博客 技术挖掘者 remanented 文章1 论文题目:Ma ...
- LTMU论文解析
LTMU 第零部分:前景提要 一般来说,单目标跟踪任务可以从以下三个角度解读: A matching/correspondence problem.把其视为前后两帧物体匹配的任务(而不考虑在跟踪过程中 ...
- CVPR2020论文解析:实例分割算法
CVPR2020论文解析:实例分割算法 BlendMask: Top-Down Meets Bottom-Up for Instance Segmentation 论文链接:https://arxiv ...
- 人脸真伪验证与识别:ICCV2019论文解析
人脸真伪验证与识别:ICCV2019论文解析 Face Forensics++: Learning to Detect Manipulated Facial Images 论文链接: http://o ...
- 人体姿态和形状估计的视频推理:CVPR2020论文解析
人体姿态和形状估计的视频推理:CVPR2020论文解析 VIBE: Video Inference for Human Body Pose and Shape Estimation 论文链接:http ...
- 视频教学动作修饰语:CVPR2020论文解析
视频教学动作修饰语:CVPR2020论文解析 Action Modifiers: Learning from Adverbs in Instructional Videos 论文链接:https://a ...
- 分层条件关系网络在视频问答VideoQA中的应用:CVPR2020论文解析
分层条件关系网络在视频问答VideoQA中的应用:CVPR2020论文解析 Hierarchical Conditional Relation Networks for Video Question ...
- 慢镜头变焦:视频超分辨率:CVPR2020论文解析
慢镜头变焦:视频超分辨率:CVPR2020论文解析 Zooming Slow-Mo: Fast and Accurate One-Stage Space-Time Video Super-Resol ...
- CVPR2020论文解析:视觉算法加速
CVPR2020论文解析:视觉算法加速 GPU-Accelerated Mobile Multi-view Style Transfer 论文链接:https://arxiv.org/pdf/2003 ...
- CVPR2020论文解析:视频语义检索
CVPR2020论文解析:视频语义检索 Fine-grained Video-Text Retrieval with Hierarchical Graph Reasoning 论文链接:https:/ ...
随机推荐
- Qt音视频开发37-识别鼠标按下像素坐标
一.前言 在和视频交互过程中,用户一般需要在显示视频的通道上点击对应的区域,弹出对应的操作按钮,将当前点击的区域或者绘制的多边形区域坐标或者坐标点集合,发送出去,通知其他设备进行处理.比如识别到很多人 ...
- UML之类型
类型是对一个元素能够拥有的值的描述.类型可能是一个无限的集合,例如Integers类型(整数),理论上它的值有无限个:也可能是一个有限的集合,例如Boolean类型(布尔),它只有True和False ...
- JSON字符串反序列化 动态泛型
需求:定时任务扫描,反射调用目标对象,但是,方法的传参不是固定的. 方案一:将方法参数存成JSON字符串,然后JSON反序列化成对象,然后反射调用 目标方法时这样的: CommandResp send ...
- 即时通讯技术文集(第15期):IM跨平台和社交软件红包技术 [共19篇]
为了更好地分类阅读 52im.net 总计1000多篇精编文章,我将在每周三推送新的一期技术文集,本次是第15 期. [- 1 -] IM跨平台技术学习(一):快速了解新一代跨平台桌面技术--Elec ...
- 记录一下关于谷歌浏览器的开发者插件之vue-devtools
在做vue进行开发的时候增加一个浏览器的插件进行开发可以做到游鱼得水,更加的舒适 在这里我留下一个git地址用来下载插件包 https://gitee.com/zhang_banglong/vue-d ...
- springboot+springsecurity项目
https://blog.csdn.net/qq_36748248/article/details/120932954 https://blog.csdn.net/weixin_41207479/ar ...
- MySQL---约束、主从复制原理、Docker搭建
MySQL(11)---约束 含义: 一种限制,用于限制表中的数据,为了保证表中的数据的准确和可靠性. 先把Mysql几种约束列出来: 主键约束 外键约束 唯一性约束 非空约束 默认值约束 自增约束 ...
- Spring Cloud认知学习(一)--Eureka使用、Ribbon使用
Spring Cloud是一个微服务架构,他有多种组件来管理微服务的方方面面.Spring Cloud是用于构建微服务开发和治理的框架的集合. Spring Cloud是最热门的Java技术毋庸置疑. ...
- G1原理—7.G1的GC日志分析解读
大纲 1.TLAB的GC日志解读 2.YGC的GC日志解读 3.模拟YGC(单次GC及多次GC的不同场景) 4.打开实验选项查看YGC的详情日志信息 5.Mixed GC日志信息之初始标记过程 6.M ...
- ctfshow--web14 sql注入利用``的清奇的绕过
输入c=3就会跳出来这个url 复制并访问,看这个页面应该是sql注入 有注释可看,看看他过滤了哪些东西 点击查看代码 if(preg_match('/information_schema\.tabl ...
