【CSP模拟赛】坏天平（数学&思维）

蹭兄弟学校的题目做还不用自己出题的感觉是真的爽

题目描述

nodgd有一架快要坏掉的天平，这架天平右边的支架有问题，如果右边的总重量比左边多太多，天平就彻底坏掉了。现在nodgd手上有n种砝码，质量分别为m⁰,m¹,m²,...,m^n-1,每种砝码有k个。现在要把这n×k个砝码逐个放到天平上，每个砝码都可以放到天平的左边或者右边。放砝码的过程中，天平右边的总重量减去左边的总重量，必须严格小于已经放上天平的最重的一个砝码。如果L,R分别表示已经放上天平左边和右边砝码质量的可重集合，则任何时候都要满足

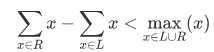
nodgd想知道放砝码的方案总数，答案mod 998,244,353后的值。两种放砝码的方法如果每次放上的砝码质量和放的位置都一样，则认为是相同的。输入格式输入文件。输入一行，包含三个正整数，含义如题目描述中所述。输出格式输出文件输出一个整数，放砝码方案总数后的值。

输入格式

输入一行，包含三个正整数n,m,k,含义如题目描述中所述。

输出格式

输出一个整数，放砝码方案总数mod 998,244,353后的值。

输入样例
2 2 1
输出样例
3

样例说明
质量为1,2的砝码各有1个。如果先放质量为1的砝码，则两个砝码都只能放左边，有1种方案。如果先放质量为2的砝码再放质量为1的砝码，则质量为2的砝码只能放左边，质量为1的砝码随便放，有2种方案。共3种方案。
数据规模与约定
对于30%的数据，n×k<=12；
对于另外20%的数据，m=2,k=1；
对于另外另外20%的数据，m=3,k=2；
对于100%的数据，1≤n×k≤10⁷,k<m≤10⁷。

分析

这道题我们拿到题目的版本要简单一些，是这个亚子的

（你™怎么连人名都换了）

所以我们先来证明一下在这个题目中

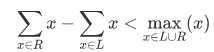
与最重的砝码个数左边应该不小于右边是等价的

对于一个质量为mⁱ砝码，我们可以发现，它的质量其实是比所有比它质量小的砝码的质量之和还要大的，

所有比它质量小的砝码的质量之和可表示为

k×(m⁰+m¹+m²+m³+m⁴+...+mⁱ^-1)=k×$\frac {m^i-m^0}{m-1}$

显然这个函数随k单调递增，又因为k<m，即k最大为m-1

所以最大值为

k×$\frac {m^i-m^0}{m-1}$ =（m-1）×$\frac {m^i-m^0}{m-1}$ =mⁱ-m⁰<mⁱ

所以天平是否会坏掉只与当前最大砝码的摆放方式有关。

然而这只是这个题目的第一步

接下来我们开始正片

对于这种看一眼就很懵不知道怎么搞的题，我们可以考虑递推

如果固定n，由k推到k+1，增加的砝码质量都不同，不是很好推，所以考虑固定k由n推到n+1

我们试着从有n-1种砝码，每种砝码k个的情况推到n种砝码，每种砝码k个的情况。

设ans_i表示i种砝码，每种砝码k个的方案数

不妨假设新增加的k个砝码是质量最小的那一堆（因为不会推最大的那一堆

那么根据样例的提示，对于第一个放上去的砝码进行讨论就有两种情况，一种是第一个放新增加，同时也是质量最小的砝码

另一种是放其它的，也是质量比新加的砝码质量要大的砝码。

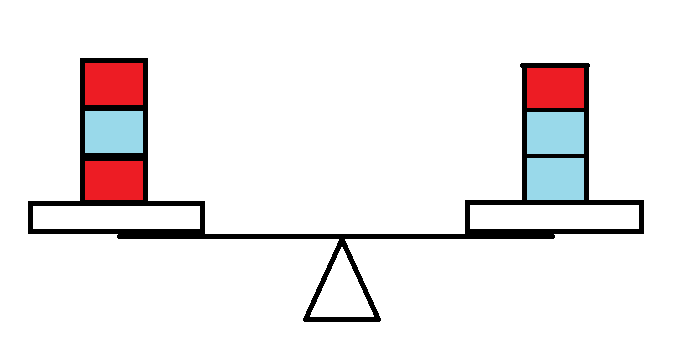
如图，蓝色表示新的，红色表示以前的。

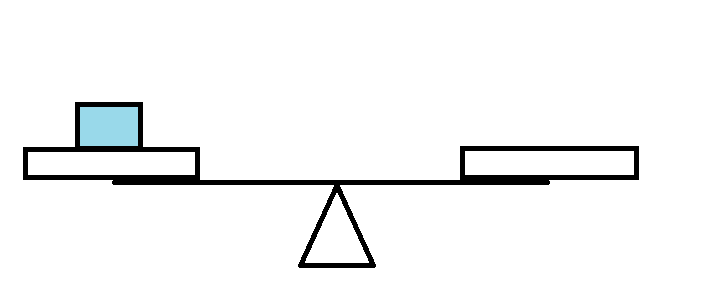
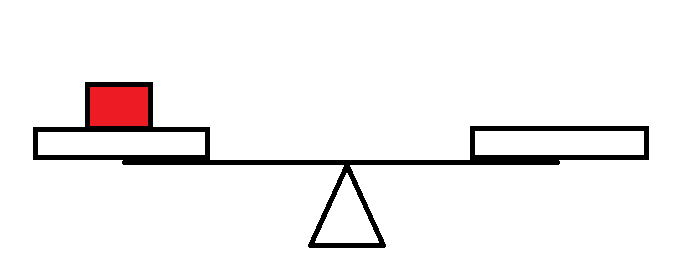
情形一情形二

对于第二种情况，天平是否会坏掉从一开始就与我们新增加的砝码无关，因为它们质量最小，

而天平是否会坏掉只与当前最大砝码的摆放方式有关。

所以这些砝码是可以乱放的，可以看作是插入到之前的砝码之中，但不能放到开头，而且每种砝码有左右两种选择

第二种情况的方案数就是ans_n-1*C(nk-1,k)*2^k

再回头来看看第一种情况，反正我还是觉得没什么思路

不过我们可以把第二种情形扩展一下，让它普遍一些。

第二种情况相当于在放第1个砝码的时候就放了质量比新增加的砝码大的砝码

而第一种情况相当于在放第i+1个砝码的时候就放了质量比新增加的砝码大的砝码（1≤i≤k）

两种情况合起来就是在放第i+1个砝码的时候就放了质量比新增加的砝码大的砝码（0≤i≤k）

那么就剩下k-i个砝码可以在以后乱放。

而前i个砝码的放置一定是合法的。

我们设f(i)表示i个同种砝码放置合法的方案数

那么总的方案数就是

ans_n=ans_n-1$\sum_{i=0}^k f(i) C_{nk-i-1}^{k-i}2^{k-i}$

只要知道f(i)就可以知道递推式了

而且ans₁=f(k)

所以只要知道f(i)就可以计算答案

接下来我们来推一下f（i）

既然f(i)表示i个同种砝码放置合法的方案数

合法的意思就是左边的砝码不少于右边砝码

感觉有点像卡特兰数

我们可以用几何法解决

如果假设放左边一个砝码相当于向右走一步，放右边一个砝码相当于向上走一步

那么f(i)就表示从（0,0）走到直线x+y=i(y>=0)且不能越过直线x=y的方案数

越过x=y的情况时肯定到达了y=x+1(绿色直线)

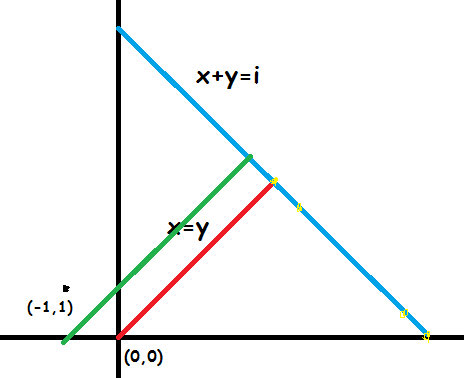
作（0,0）关于y=x+1的对称点（-1,1），那么f（i）就是（0,0）走到黄色点的方案数-（-1,1）走到黄色点的方案数（有些黄色点没画）

所以

f（i）=C(i,i/2)-C(i,i/2+1)+C(i,i/2+1)-C(i,i/2+2).....+C(i,0)-C(i,-1)

=C(i,i/2)-C(i,-1)

=C(i,i/2)

我们终于可以得出答案

ans₁=C_{k}^{k/2}

ans_n=ans_n-1$\sum_{i=0}^k f(i) C_{nk-i-1}^{k-i}2^{k-i}$

时间复杂度为O(nk)

分析过程贼长但最后依然还是挺短的代码

#include<cstdio>

#include<algorithm>

using namespace std;

const int maxn=;

const int mod=;

int n,m,k,ans,fac[maxn],inv[maxn],bw[maxn],f[maxn];

int qp(int a,int k)

{

    int res=;

    while(k){if(k&)res=1ll*res*a%mod;a=1ll*a*a%mod;k>>=;}

    return res;

}

void prework()

{

    bw[]=fac[]=;

    for(int i=;i<=;i++)bw[i]=2ll*bw[i-]%mod,fac[i]=1ll*i*fac[i-]%mod;

    inv[]=qp(fac[],mod-);

    for(int i=;i>=;i--)inv[i]=1ll*(i+)*inv[i+]%mod;

}

int C(int a,int b){return 1ll*fac[a]*inv[a-b]%mod*inv[b]%mod;}

int main()

{

    scanf("%d%d%d",&n,&m,&k);

    prework();ans=C(k,k/);

    for(int i=;i<=n;i++)

    {

        int t=;

        for(int j=;j<=k;j++)

            t=(t+1ll*C(j,j/)*bw[k-j]%mod*C(i*k-j-,k-j)%mod)%mod;

        ans=1ll*ans*t%mod;

    }

    printf("%d\n",ans);

}