OpenFOAM——孔板流量计
本算例来自《ANSYS FLUENT技术基础与工程应用:流动传热与环境污染控制领域》
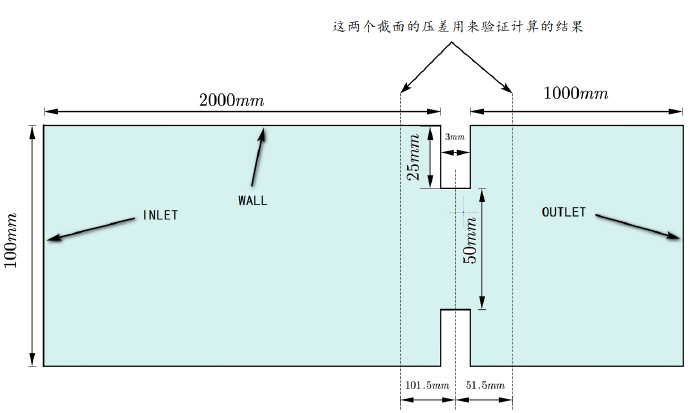
一个入口,入口速度为0.0176839m/s,一个出口边界,其余为壁面边界
流体的物性参数:
密度:1000kg/m3
动力黏度:0.001kg/(m·s)
运动黏度:0.000001m2/s
本算例采用kOmegaSST湍流模型进行计算,请注意第一层网格的高度。
首先进行建模操作,任何建模软件均可,本算例采用ICEM直接建模,生成网格,缩放网格,然后利用OpenFOAM下转化网格,划分完成的网格如下:


接下来转入OpenFOAM的操作:
首先新建一个文件夹,名字任取,用来作为算例文件夹,本算例中我将该文件夹命名为:flowmeter_3D

然后进入OpenFOAM的安装目录,将安装目录下的motorBike算例(我的目录为/opt/openfoam5/tutorials/incompressible/simpleFoam/motorBike)下的0文件夹、constant文件夹和system文件夹拷贝到flowmeter_3D文件夹下,然后将0.org文件夹重命名为0,删除该文件夹下的include文件夹

删除constant文件夹下的triSurface文件夹

在system目录下删除下面截图中的文件
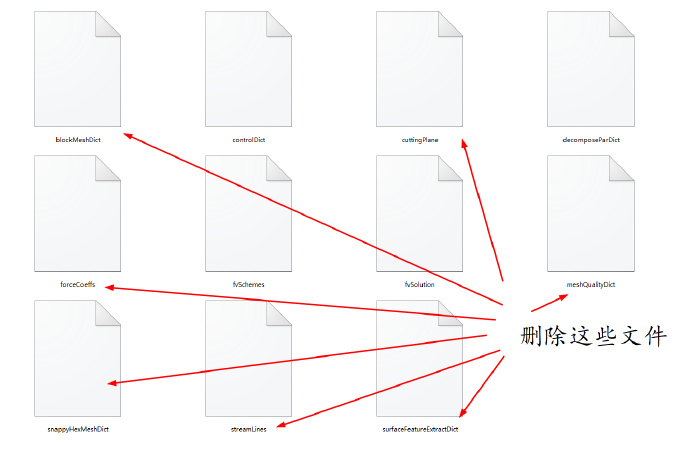
然后我们将刚才我们生成的.msh网格拷贝到flowmeter_3D文件夹下。在算例文件夹下打开终端,由于是三维模型,我们输入fluent3DMeshToFoam命令(本算例也可以使用fluentMeshToFoam来实现网格转换):


我们打开constant文件夹下的transportproperties文件,内容修改如下:
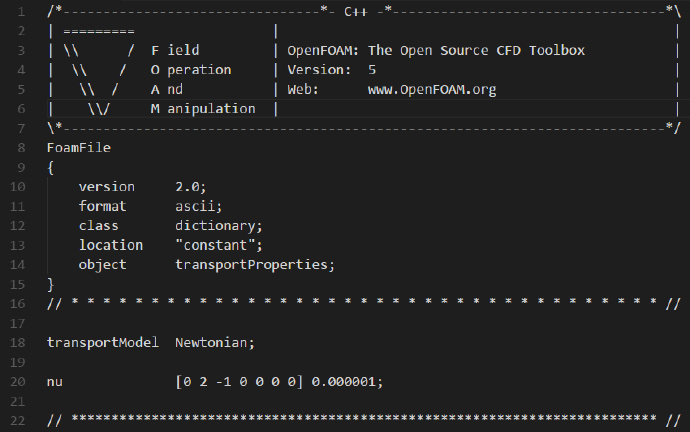
接下来,修改turbulenceProperties文件的内容如下:
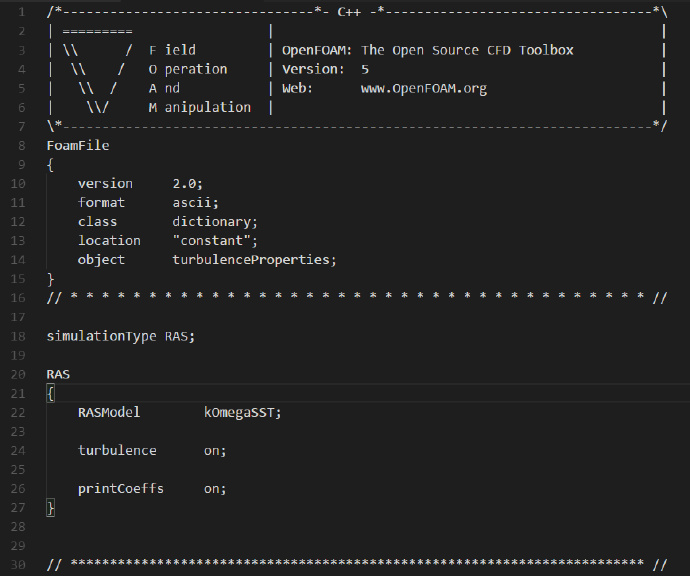
转入0文件夹
p文件当中的内容如下:

注意一下,此处的压力是运动压力,压力除以了密度
U文件当中的内容如下:

说明一下:
surfaceNormalFixedValue
基本格式为
边界名称
{
type surfaceNormalFixedValue;
refValue uniform 数值;
}
说明:
该边界类型指定垂直于边界流入流出计算域物理量的值,数值为整数时表示流出计算域,为负数时表示流入计算域
k文件当中的内容如下:

说明一下:
turbulentIntensityKineticEnergyInlet
基本格式:
边界名称
{
type turbulentIntensityKineticEnergyInlet;
intensity 数值;
value uniform 数值/$internalField;
}
说明:
可通过湍流强度来k的值,value关键字下可填写任意数值或$internalField(仅是将字符串拷贝到本地,等于内部场的值),仅起到占位的作用,并不对计算造成影响。很显然在壁面处,k应该为0。
omega文件当中的内容如下:

说明一下:
omegaWallFunction
基本格式:
边界名称
{
type omegaWallFunction;
value uniform 数值
}
说明:
该边界条件仅对壁面设置壁面函数,应用在kOmega或kOmegaSST湍流模型中,从而对方程进行求解。value关键字下可填写任意数值或$internalField(仅是将字符串拷贝到本地,等于内部场的值),仅起到占位的作用,并不对计算造成影响。
turbulentMixingLengthFrequencyInlet
基本格式:
边界名称
{
type turbulentMixingLengthFrequencyInlet;
mixingLength 数值;
value uniform 数值;
}
说明:
可通过混合长度来计算omega(ω)的值,value关键字下可填写任意数值或$internalField(仅是将字符串拷贝到本地,等于内部场的值),仅起到占位的作用,并不对计算造成影响。mixingLength为湍流尺度,其计算公式为:I=0.007L(其中I为mixingLength的值,L为特征尺寸)。
nut文件当中的内容如下:

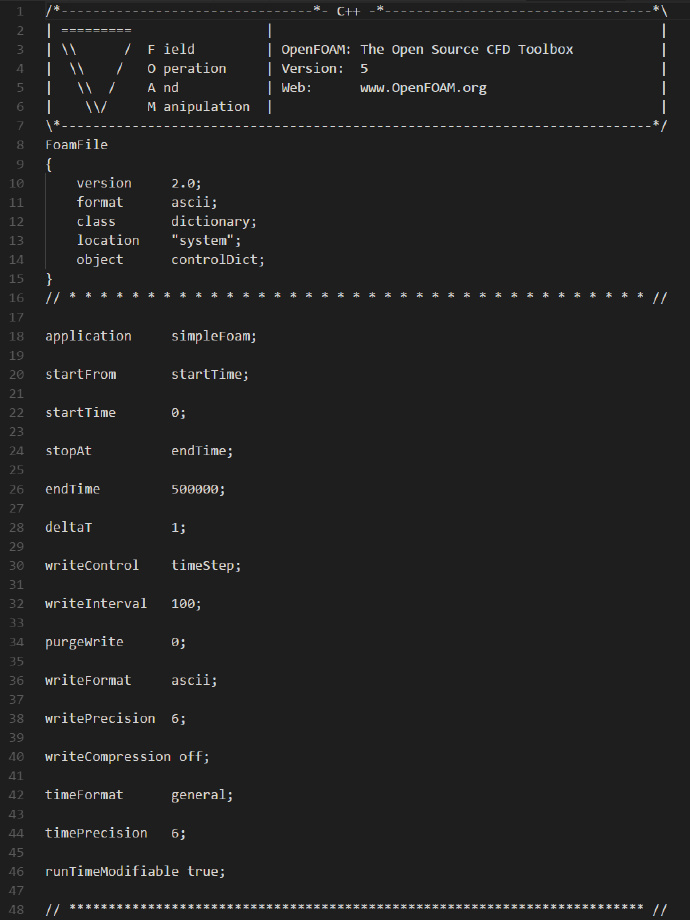
接着我们设置system文件夹下的controlDict文件:
fvSchemes文件修改如下:

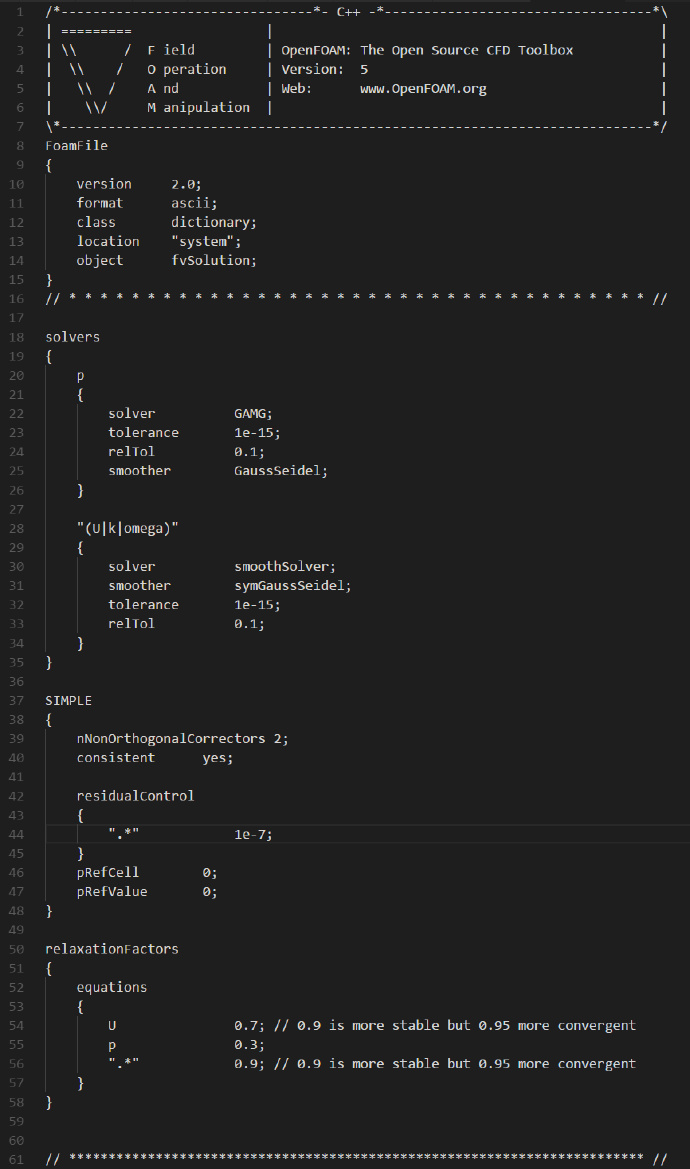
fvSolution文件修改如下:
为了加快计算速度,我们采用分块并行的计算方法,我们在system目录下新建decomposeParDict来分块,decomposeParDict中的内容为:

输入decomposePar进行分块


由于我安装了PyFoam来实时输出残差,所以在终端中输入pyFoamPlotRunner.py --clear --proc=16 simpleFoam开始计算

等到计算结束

中心切面云图

管道中流体的实际体积流量qv的计算式如下:


式中:
β——孔板流量计的直径比,本算例为0.5
△p’——为取样界面之间的压差,本算例取孔板上游100mm处和孔板下游50mm处界面的压差
ρ——流体密度
我们在ParaView当中分别取两个面的平均压力,操作如下:
首先paraFoam启动ParaView

然后我们首先截取孔板上游100mm的截面




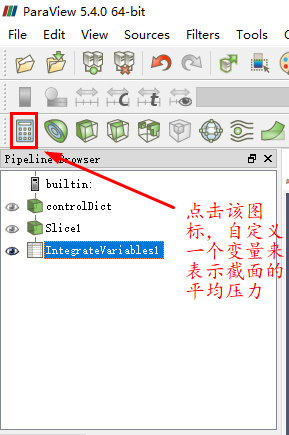




然后我们重复上面的步骤去下游50mm截面处的平均压力


截面之间运动压力之差=0.00407066-(-0.00156585)
=0.00563651m2/s2
带入上面的计算公式可得流出系数:
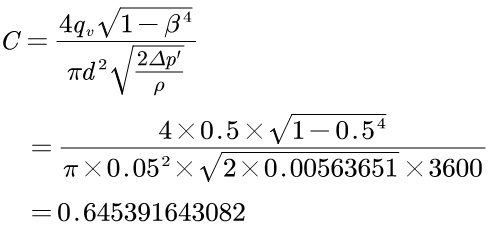

ISO公式计算流出系数为C=0.6526
两者之间的误差为
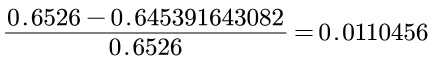
OpenFOAM——孔板流量计的更多相关文章
- 【一起学OpenFOAM】03 OpenFOAM基本使用流程
OpenFOAM初学者常常对于软件的使用流程感到很迷惑,与其他的具有GUI的CFD软件不同,OpenFOAM的所有操作均为基于文本操作,譬如说里面各种计算模型.计算参数.流程控制参数等,均为通过修改对 ...
- 【一起学OpenFOAM】系列由来
1 为什么要学习OpenFOAM 掐指算起来,接触CFD也差不多有十个年头了,其间一直使用的商用CFD软件,有Fluent.CFX.StarCCM+等,这些商用软件各有其优缺点,都能较好的解决常规的工 ...
- 【一起学OpenFoam】02 软件准备
"工欲善其事必先利其器",在利用OpenFoam解决我们的工程问题之前,首先要做的事情是搭建一个OpenFoam运行环境.很遗憾的是,OpenFoam的原生开发系统是Linux,因 ...
- OpenSUSE下编译安装OpenFoam
在不是Ubuntu系统下安装OpenFoam,需要采用编译安装的方式.以下以OpenSuSE为例进行编译安装. 1 软件包准备 需要下载两个程序包: OpenFOAM-4.x-version-4.1. ...
- 【一起学OpenFoam】01 OpenFoam的优势
CFD技术发展到今天,已经超过了大半个世纪了,已经涌现出非常多的CFD软件可供人们使用.通用商业CFD软件譬如Fluent.CFX.Star CCM+等在工业上得到了广泛的应用,另外一些专用的软件(如 ...
- OpenFOAM&Gmsh&CFD圆柱绕流(两个圆柱)
问题: 圆柱绕流问题,模拟仿真有两个圆柱.一个源的流体变化情况. 解决步骤: 1.使用Gmsh画出网格,并保存cylindertwo.msh 2.以Cavity为基础创建新的Case:Cylinder ...
- OpenFOAM 学习路线 【转载】
"Two weeks of playing with a CFD code will save you one afternoon of reading" 什么是OpenFOAM( ...
- openfoam 的安装【转载】
原文地址: http://blog.sina.com.cn/s/blog_14bf001d10102wifw.html OpenFOAM安装 OpenFOAM基于Linux系统下运行,由于对Linux ...
- 【一起学OpenFOAM】04 OpenFOAM的学习资源
OpenFOAM的学习资料并不多,个人猜测也许是与软件的类型有关系. 对于商用软件来讲,由于要占领市场,软件开发商自然是巴不得会用软件的人越多越好,因为他们卖的是软件,会用的人越多,软件卖得越好.他们 ...
随机推荐
- C# 实用代码段
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; usin ...
- WindowsXP序列号产生原理(椭圆曲线法)
WindowsXP序列号产生原理(椭圆曲线法) 来源 https://blog.csdn.net/zhiyuan411/article/details/5156330 参考 https://www. ...
- ios app UI自动化测试用到的命令
ios测试的app测试包,真机设备需要开发者证书并且将测试机的udid加入到pp文件文件,configruation 要求为debug模式的ipa包, 1.苹果手机的UDID, a.通过 xcode- ...
- 米尔XC7Z010开发板资源
关于XC7Z010开发板 详细介绍http://www.myir-tech.com/product/myc_C7Z010_20.htm Xilinx基于28nm工艺流程的Zynq-7000 All P ...
- Linux应急响应姿势浅谈
一.前记 无论是甲方还是乙方的同学,应急响应可能都是家常便饭,你可能经常收到如下反馈: 运维同事 --> 服务器上存在可疑进程,系统资源占用高: 网络同事 --> 监控发现某台服务器对外大 ...
- Js字符串用法
js字符串整理导向图 ---欢迎收藏^ - ^
- 一步一步实现kbmmw的httpsys使用https功能
kbmmw的httpsys的功能已经实现了好长时间,但是现在各个平台都要求使用https来提供服务. 今天一步一步来说一下如何使用kbmmw 的httpsys功能支持https. 首先为了获得证书,我 ...
- OSPF 多区域配置
通过配置OSPF协议使网络互通. 实验拓扑 如图所示连接,地址规划如下: 名称 接口 IP地址 R1 f1/0 192.168.10.1/24 R1 f0/0 192.168.20.1/24 R1 f ...
- Werkzeug——python web开发工具包
转载请注明原文地址:https://www.cnblogs.com/ygj0930/p/10826062.html 一:Werkzeug是个啥 1)Werkzeug是一个工具包,它封装了很多东西,诸如 ...
- Web服务基础介绍
Web服务基础介绍 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 一.正常情况下的单次web服务访问流程 博主推荐阅读: https://www.cnblogs.com/yinzh ...
