Arrays的排序算法sort及方法使用

　　Java工具包中的Arrays工具类里面有数组的快速排序算法。

源码如下：

 /**
      * Sorts the specified range of the array using the given
      * workspace array slice if possible for merging
      *
      * @param a the array to be sorted
      * @param left the index of the first element, inclusive, to be sorted
      * @param right the index of the last element, inclusive, to be sorted
      * @param work a workspace array (slice)
      * @param workBase origin of usable space in work array
      * @param workLen usable size of work array
      */
     static void sort(int[] a, int left, int right,
                      int[] work, int workBase, int workLen) {
         // Use Quicksort on small arrays
         if (right - left < QUICKSORT_THRESHOLD) {
             sort(a, left, right, true);
             return;
         }

         /*
          * Index run[i] is the start of i-th run
          * (ascending or descending sequence).
          */
         int[] run = new int[MAX_RUN_COUNT + 1];
         int count = 0; run[0] = left;

         // Check if the array is nearly sorted
         for (int k = left; k < right; run[count] = k) {
             if (a[k] < a[k + 1]) { // ascending
                 while (++k <= right && a[k - 1] <= a[k]);
             } else if (a[k] > a[k + 1]) { // descending
                 while (++k <= right && a[k - 1] >= a[k]);
                 for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) {
                     int t = a[lo]; a[lo] = a[hi]; a[hi] = t;
                 }
             } else { // equal
                 for (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) {
                     if (--m == 0) {
                         sort(a, left, right, true);
                         return;
                     }
                 }
             }

             /*
              * The array is not highly structured,
              * use Quicksort instead of merge sort.
              */
             if (++count == MAX_RUN_COUNT) {
                 sort(a, left, right, true);
                 return;
             }
         }

         // Check special cases
         // Implementation note: variable "right" is increased by 1.
         if (run[count] == right++) { // The last run contains one element
             run[++count] = right;
         } else if (count == 1) { // The array is already sorted
             return;
         }

         // Determine alternation base for merge
         byte odd = 0;
         for (int n = 1; (n <<= 1) < count; odd ^= 1);

         // Use or create temporary array b for merging
         int[] b;                 // temp array; alternates with a
         int ao, bo;              // array offsets from 'left'
         int blen = right - left; // space needed for b
         if (work == null || workLen < blen || workBase + blen > work.length) {
             work = new int[blen];
             workBase = 0;
         }
         if (odd == 0) {
             System.arraycopy(a, left, work, workBase, blen);
             b = a;
             bo = 0;
             a = work;
             ao = workBase - left;
         } else {
             b = work;
             ao = 0;
             bo = workBase - left;
         }

         // Merging
         for (int last; count > 1; count = last) {
             for (int k = (last = 0) + 2; k <= count; k += 2) {
                 int hi = run[k], mi = run[k - 1];
                 for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) {
                     if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) {
                         b[i + bo] = a[p++ + ao];
                     } else {
                         b[i + bo] = a[q++ + ao];
                     }
                 }
                 run[++last] = hi;
             }
             if ((count & 1) != 0) {
                 for (int i = right, lo = run[count - 1]; --i >= lo;
                     b[i + bo] = a[i + ao]
                 );
                 run[++last] = right;
             }
             int[] t = a; a = b; b = t;
             int o = ao; ao = bo; bo = o;
         }
     }

　　java.util.Arrays类能方便的操作数组，它所有的方法都是静态的。

　　1.filll方法 ：给数组中的某段元素附上相同值。

　　2.sort方法：对数组中某段元素排序。

　　3.equals方法：比较两个数组，判断的是数组中元素值是否相等。

　　4.binarySearch方法：对排过序的数组进行二分法查找。

测试用例：

 package recursion;

 import java.util.Arrays;

 /**
  * @author zsh
  * @company wlgzs
  * @create 2019-02-17 9:33
  * @Describe Arrays方法测试
  */
 public class TestForArrays {

     public static void main(String[] args) {
         //填充数组，将arr[]中所有元素的值初始为0
         int[] arr = new int[5];
         Arrays.fill(arr,12);
         System.out.println(Arrays.toString(arr));
         //将arr中的第2个到第三个元素的值赋为8
         Arrays.fill(arr,1,3,8);
         System.out.println(Arrays.toString(arr));
         //对数组进行排序
         int[] arr1 = new int[]{7,6,8,5,2,9,8,1,3,5};
         //对数组的第二个到第6个元素进行排序
         Arrays.sort(arr1,1,6);
         System.out.println(Arrays.toString(arr1));
         //对整个数组进行排序
         Arrays.sort(arr1);
         System.out.println(Arrays.toString(arr1));
         //比较数组元素是否相等
         System.out.println(Arrays.equals(arr,arr1));
         //使用二分法在数组中查找指定元素所在的下标
         //数组必须是先排好序的
         System.out.println(Arrays.binarySearch(arr1,5));
         //如果不存在，就返回负数
         System.out.println(Arrays.binarySearch(arr1,20));
     }

 }

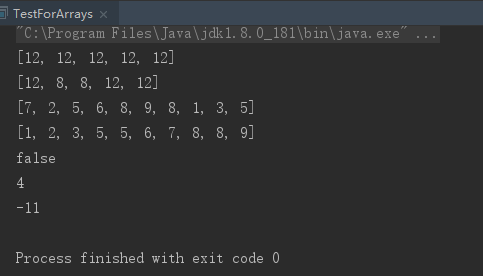
控制台输出：