Dirichlet分布深入理解
Dirichlet分布
我们把Beta分布推广到高维的场景,就是Dirichlet分布。Dirichlet分布定义如下
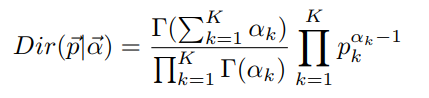
Dirichlet分布与多项式分布共轭。多项式分布定义如下

共轭关系表示如下
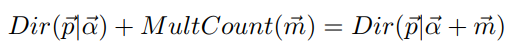
Dirichlet-MultCount共轭理解
上述共轭关系我们可以这样理解,先验Dirichlet分布参数为α,多项式分布实验结果为m,则后验Dirichlet分布的参数为α+m。m为n维向量,表示实验中各种结果出现的次数。例如投掷骰子的试验中,m为6维向量,6个分量分别表示出现1点到6点的次数。
一般来说,我们使用贝叶斯定理推断Dirichlet-MultCount共轭关系。对于参数为α的Dirichlet分布,可以用如下公式表示
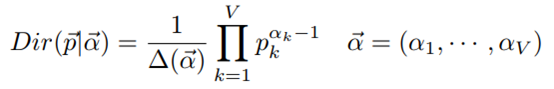
这里,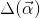 表达式如下
表达式如下
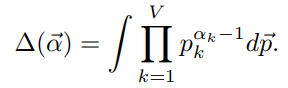
进行了多项式分布实验后,得到结果n后,后验分布为

参数n与α确定后,后验分布的期望为

Dirichlet分布深入理解的更多相关文章
- 关于Beta分布、二项分布与Dirichlet分布、多项分布的关系
在机器学习领域中,概率模型是一个常用的利器.用它来对问题进行建模,有几点好处:1)当给定参数分布的假设空间后,可以通过很严格的数学推导,得到模型的似然分布,这样模型可以有很好的概率解释:2)可以利用现 ...
- LDA-math-认识Beta/Dirichlet分布
http://cos.name/2013/01/lda-math-beta-dirichlet/#more-6953 2. 认识Beta/Dirichlet分布2.1 魔鬼的游戏—认识Beta 分布 ...
- 机器学习的数学基础(1)--Dirichlet分布
机器学习的数学基础(1)--Dirichlet分布 这一系列(机器学习的数学基础)主要包括目前学习过程中回过头复习的基础数学知识的总结. 基础知识:conjugate priors共轭先验 共轭先验是 ...
- mahout系列----Dirichlet 分布
Dirichlet分布可以看做是分布之上的分布.如何理解这句话,我们可以先举个例子:假设我们有一个骰子,其有六面,分别为{1,2,3,4,5,6}.现在我们做了10000次投掷的实验,得到的实验结果是 ...
- 伯努利分布、二项分布、Beta分布、多项分布和Dirichlet分布与他们之间的关系,以及在LDA中的应用
在看LDA的时候,遇到的数学公式分布有些多,因此在这里总结一下思路. 一.伯努利试验.伯努利过程与伯努利分布 先说一下什么是伯努利试验: 维基百科伯努利试验中: 伯努利试验(Bernoulli tri ...
- (转)机器学习的数学基础(1)--Dirichlet分布
转http://blog.csdn.net/jwh_bupt/article/details/8841644 这一系列(机器学习的数学基础)主要包括目前学习过程中回过头复习的基础数学知识的总结. 基础 ...
- Beta分布和Dirichlet分布
在<Gamma函数是如何被发现的?>里证明了\begin{align*} B(m, n) = \int_0^1 x^{m-1} (1-x)^{n-1} \text{d} x = \frac ...
- LDA学习之beta分布和Dirichlet分布
---恢复内容开始--- 今天学习LDA主题模型,看到Beta分布和Dirichlet分布一脸的茫然,这俩玩意怎么来的,再网上查阅了很多资料,当做读书笔记记下来: 先来几个名词: 共轭先验: 在贝叶斯 ...
- 联邦学习:按Dirichlet分布划分Non-IID样本
我们在<Python中的随机采样和概率分布(二)>介绍了如何用Python现有的库对一个概率分布进行采样,其中的dirichlet分布大家一定不会感到陌生.该分布的概率密度函数为 \[P( ...
随机推荐
- Docker 容器(六)
镜像(Image)和容器(Container)的关系,就像是面向对象程序设计中的 类 和 实例 一样,镜像是静态的定义,容器是镜像运行时的实体.容器可以被创建.启动.停止.删除.暂停等. 容器的实质是 ...
- yaml语言在线可视化翻译
yaml语言在线可视化翻译 https://editor.swagger.io/
- 【叶问】 MySQL常用的sql调优手段或工具有哪些
MySQL常用的sql调优手段或工具有哪些1.根据执行计划优化 通常使用desc或explain,另外可以添加format=json来输出更详细的json格式的执行计划,主要注意点如下: ...
- 如何把Composer镜像迁移到Laravel China 维护的镜像?
今天在更新Laravel-admin:1.6.0提示没有对应的包,后面才发现需要使用官方或者 Laravel-China 的 composer 镜像,phpcomposer 镜像已经停止维护了.怎么从 ...
- Openresty 安装第三方插件
Openresty 安装第三方插件 程序媛没有夜生活 2016.08.02 15:33* 字数 167 阅读 1283评论 0喜欢 2 在安装之前,我们先来看一下我们现有的模块. 1.将需要安装的插件 ...
- mybatis {arg0} 与 {0}
解决方案: MyBatis的XML的配置文件中声明设置属性的useActualParamName参数值为假 <setting name="useActualParamName" ...
- 《全栈性能Jmeter》-2性能测试初体验
- @Value("#{}") 和 @Value("{}")
1 @Value("#{}") SpEL表达式 @Value("#{}") 表示SpEl表达式通常用来获取bean的属性,或者调用bean的某个方法.当然还 ...
- SEO--网站流量提升
话术设置,提炼优质的话术 关键词的挖掘 1.头脑风暴 (开晨会,一堆人坐在一起聊.) 2.利用搜索引擎相关搜索(将关键词设置为搜索热词,利用工具:百度指数,查看关键词) 3.工具 4.长尾关键词(词比 ...
- MySQL学习笔记--启动停止服务
右键点击计算机->管理->服务 windows所有的服务都在,mysql等等.可以在这里启动停止服务也可以在命令行 net start/stop <服务名> InnoDB还 ...
