Codeforces 798D Mike and distribution - 贪心

Mike has always been thinking about the harshness of social inequality. He's so obsessed with it that sometimes it even affects him while solving problems. At the moment, Mike has two sequences of positive integers A = [a₁, a₂, ..., a_n] and B = [b₁, b₂, ..., b_n] of length n each which he uses to ask people some quite peculiar questions.

To test you on how good are you at spotting inequality in life, he wants you to find an "unfair" subset of the original sequence. To be more precise, he wants you to select k numbers P = [p₁, p₂, ..., p_k] such that 1 ≤ p_i ≤ n for 1 ≤ i ≤ k and elements in P are distinct. Sequence P will represent indices of elements that you'll select from both sequences. He calls such a subset P "unfair" if and only if the following conditions are satisfied: 2·(a_p1 + ... + a_pk) is greater than the sum of all elements from sequence A, and 2·(b_p1 + ... + b_pk) is greater than the sum of all elements from the sequence B. Also, k should be smaller or equal to 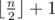because it will be to easy to find sequence P if he allowed you to select too many elements!

Mike guarantees you that a solution will always exist given the conditions described above, so please help him satisfy his curiosity!

Input

The first line contains integer n (1 ≤ n ≤ 10⁵) — the number of elements in the sequences.

On the second line there are n space-separated integers a₁, ..., a_n (1 ≤ a_i ≤ 10⁹) — elements of sequence A.

On the third line there are also n space-separated integers b₁, ..., b_n (1 ≤ b_i ≤ 10⁹) — elements of sequence B.

Output

On the first line output an integer k which represents the size of the found subset. k should be less or equal to .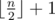

On the next line print k integers p₁, p₂, ..., p_k (1 ≤ p_i ≤ n) — the elements of sequence P. You can print the numbers in any order you want. Elements in sequence P should be distinct.

Example

Input

58 7 4 8 34 2 5 3 7

Output

3 1 4 5

---

　　题目大意 给定两个长度为n的数列，选出不多于$\left \lfloor \frac{n}{2} \right \rfloor + 1$个互不相同的下标，使得每个数组对应下标的数的和的两倍超过它的和。

　　显然贪心，我有很多稀奇古怪的想法，然后全都完美Wrong Answer。突然觉得自己可能一直用的都是假贪心，给这道题跪了。下面说正解吧。

　　这个可以看成二维贪心，对于高维问题我们通常想到的是降维，再根据常用套路，降维通常用的两种方法：排序和枚举一维。

　　因为这里是贪心，所以显然排序。

　　题目要求还可以转化成，选择一些下标，在每个数组中，被选择数之和比剩下的数的和大。

　　首先选择A[1]，然后之后每两个分为一组，每组中哪个对应的B大就选哪个。如果n为偶数，再把最后一个选上。

　　显然在B数组中是满足题目要求的(每组中都选了最大的，还多选了1个或2个)，对于A数组，每个选择了A[i]一定大于等于下一组内选择的A[j]，而且会多选1个或2个，所以A数组也满足。

Code

 /**
  * Codeforces
  * Problem#798D
  * Accepted
  * Time: 62ms
  * Memory: 4500k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;

 typedef class Data {
     public:
         int id;
         int x;
         int y;
 }Data;

 int n;
 int *A, *B;
 Data *ds;

 boolean cmp(const Data &a, const Data& b) {    return a.x > b.x;    }

 inline void init() {
     scanf("%d", &n);
     A = )];
     B = )];
     ds = )];
     ; i <= n; i++)
         scanf("%d", A + i), ds[i].x = A[i], ds[i].id = i;
     ; i <= n; i++)
         scanf("%d", B + i), ds[i].y = B[i];
 }

 vector<int> buf;
 inline void solve() {
     sort(ds + , ds + n + , cmp);
     buf.push_back(ds[].id);
     ; i < n; i += )
         buf.push_back((ds[i].y > ds[i + ].y) ? (ds[i].id) : (ds[i + ].id));
     ) == )
         buf.push_back(ds[n].id);
     printf("%d\n", (signed)buf.size());
     ; i < (signed)buf.size(); i++)
         printf("%d ", buf[i]);
 }

 int main() {
     init();
     solve();
     ;
 }