洛谷P3373 [模板]线段树 2(区间增减.乘 区间求和)

To 洛谷.3373 [模板]线段树2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.将某区间每一个数乘上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式：

输出包含若干行整数，即为所有操作3的结果。

输入输出样例

输入样例#1：

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出样例#1：

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

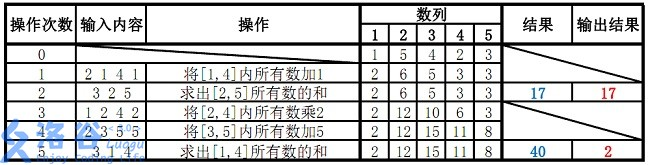
故输出应为17、2（40 mod 38=2）

代码：

 #include<cstdio>
 #define LL long long//开long long!!
 using namespace std;
 const int N=;

 int n,m,mod;
 LL Sum[N<<],LazySum[N<<],LazyMult[N<<];

 void read(int &now)
 {
     now=;int f=;char c=getchar();
     while(c<''||c>'')
     {
         if(c=='-')f=-;
         c=getchar();
     }
     while(c>=''&&c<='')now=(now<<)+(now<<)+c-'',c=getchar();
     now*=f;
 }

 void PushUp(int rt)
 {
     Sum[rt]=Sum[rt<<]+Sum[rt<<|];
 }
 void PushDown(int rt,int m)
 {
     if(LazyMult[rt]!=)//乘法标记需不为1
     {
         Sum[rt<<]*=LazyMult[rt];Sum[rt<<]%=mod;
         Sum[rt<<|]*=LazyMult[rt];Sum[rt<<|]%=mod;
         LazyMult[rt<<]*=LazyMult[rt];LazyMult[rt<<]%=mod;
         LazyMult[rt<<|]*=LazyMult[rt];LazyMult[rt<<|]%=mod;
         LazySum[rt<<]*=LazyMult[rt];LazySum[rt<<]%=mod;
         LazySum[rt<<|]*=LazyMult[rt];LazySum[rt<<|]%=mod;
         LazyMult[rt]=;
     }
     if(LazySum[rt])
     {
         Sum[rt<<]+=LazySum[rt]*(m-(m>>));Sum[rt<<]%=mod;
         Sum[rt<<|]+=LazySum[rt]*(m>>);Sum[rt<<|]%=mod;
         LazySum[rt<<]+=LazySum[rt];LazySum[rt<<]%=mod;
         LazySum[rt<<|]+=LazySum[rt];LazySum[rt<<|]%=mod;
         LazySum[rt]=;
     }
 }
 void Build(int l,int r,int rt)
 {
     LazySum[rt]=;LazyMult[rt]=;
     if(l==r)
     {
         scanf("%lld",&Sum[rt]);
         return;
     }
     int m=(l+r)>>;
     Build(l,m,rt<<);
     Build(m+,r,rt<<|);
     PushUp(rt);
 }
 void ModifyAdd(int l,int r,int rt,int L,int R,int v)
 {
     if(L<=l && r<=R)
     {
         Sum[rt]+=v*(r-l+);Sum[rt]%=mod;
         LazySum[rt]+=v;LazySum[rt]%=mod;
         return;
     }
     PushDown(rt,r-l+);
     int m=(l+r)>>;
     if(L<=m) ModifyAdd(l,m,rt<<,L,R,v);
     if(m<R) ModifyAdd(m+,r,rt<<|,L,R,v);
     PushUp(rt);
 }
 void ModifyMult(int l,int r,int rt,int L,int R,int v)
 {
     if(L<=l && r<=R)
     {//对于懒惰标记 乘法会影响加法，但加法并不会影响乘法
     //所以加法标记必须也乘
         Sum[rt]*=v;Sum[rt]%=mod;
         LazySum[rt]*=v;LazySum[rt]%=mod;//更新乘法的同时更新加法
         LazyMult[rt]*=v;LazyMult[rt]%=mod;
         return;
     }
     PushDown(rt,r-l+);
     int m=(l+r)>>;
     if(L<=m) ModifyMult(l,m,rt<<,L,R,v);
     if(m<R) ModifyMult(m+,r,rt<<|,L,R,v);
     PushUp(rt);
 }
 LL QuerySum(int l,int r,int rt,int L,int R)
 {
     if(L<=l && r<=R) return Sum[rt];
     PushDown(rt,r-l+);
     int m=(l+r)>>;LL res=;
     if(L<=m) res+=QuerySum(l,m,rt<<,L,R),res%=mod;
     if(m<R) res+=QuerySum(m+,r,rt<<|,L,R),res%=mod;
     return res;
 }

 int main()
 {
     read(n);read(m);read(mod);
     Build(,n,);
     for(int i=;i<=m;i++)
     {
         int opt,a,b;
         read(opt);read(a);read(b);
         if(opt==)
         {
             int k;read(k);
             ModifyMult(,n,,a,b,k);
         }
         else if(opt==)
         {
             int k;read(k);
             ModifyAdd(,n,,a,b,k);
         }
         else
           printf("%lld\n",QuerySum(,n,,a,b));
     }
     return ;
 }