CodeForces 568B DP Symmetric and Transitive

题意：

根据离散数学的内容知道，一个二元关系是一个二元有序组<x, y>的集合。

然后有一些特殊的二元关系，比如等价关系，满足三个条件：

• 自反性，任意的x，都有二元关系<x, x>
• 对称性，如果有<x, y>则有<y, x>
• 传递性，如果有<x, y>和<y, z>，则有<x, z>

现在要统计满足后两条，但不满足第一个条件的二元关系的个数。

题中的证明是对的：

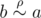If , then (according to property (2)), which means (according to property (3)).

但是前提条件不一定存在，比如对于a，没有一个b满足那么后面的推导就无从谈起了。

不妨把这些不和其他元素(包括自己)产生二元关系的元素称作「空」的。

只要至少有一个「空」的元素，而且其他的元素都在某个等价类里面，就满足题目中的要求。

枚举非「空」元素的个数k(1 ≤ k ≤ n)，选出k个元素有C(n, k)中方案，再乘上将k个元素划分为若干个等价类的方案数eq[k]，累加起来就是答案。

eq数组可以这样计算：

设d(i, j)为将i个元素划分为j个不同等价类的方案数，d(i, j) = d(i-1, j) * j + d(i-1, j-1) //考虑第i个数加入已有的j个等价类，或者自己成为一个新的等价类

那么eq[i] = sum{ d(i, j) | 0 ≤ j ≤ i }

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 using namespace std;

 typedef long long LL;

 const int maxn =  + ;
 const LL MOD = ;

 LL C[maxn][maxn], d[maxn][maxn];

 void add(LL& x, LL y)
 {
     x += y;
     if(x >= MOD) x -= MOD;
 }

 int main()
 {
     int n; scanf("%d", &n);

     for(int i = ; i <= n; i++) C[i][] = C[i][i] = ;
     for(int i = ; i <= n; i++)
         for(int j = ; j < i; j++) C[i][j] = (C[i-][j] + C[i-][j-]) % MOD;

     d[][] = ;
     for(int i = ; i <= n; i++)
         for(int j = ; j <= i; j++) d[i][j] = (d[i-][j] * j + d[i-][j-]) % MOD;

     LL ans = ;
     for(int i = ; i < n; i++)
     {
         LL eq = ;
         for(int j = ; j <= i; j++) add(eq, d[i][j]);
         ans = (ans + C[n][i] * eq) % MOD;
     }

     printf("%I64d\n", ans);

     return ;
 }

代码君