互相关（cross-correlation）及其在Python中的实现

互相关（cross-correlation）及其在Python中的实现

在这里我想探讨一下“互相关”中的一些概念。正如卷积有线性卷积（linear convolution）和循环卷积（circular convolution）之分；互相关也有线性互相关（linear cross-correlation）和循环互相关（circular cross-correlation）。线性互相关和循环互相关的基本公式是一致的，不同之处在于如何处理边界数据。其本质的不同在于它们对原始数据的看法不同。通过这篇文章，我想整理一下相关概念，并给出示例。

1. 线性相关（Linear Cross-Correlation）的定义和计算

假设我们手里有两组数据，分别为个和个，表示为：和，比长，即。序列和之间的线性互相关操作表示为，其结果也是一个序列，表示为。具体的操作是用这两个序列进行的一种类似“滑动点积”的操作，如图1和图2所示。

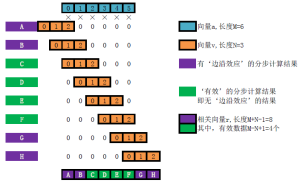
图1. 线性互相关的计算过程示意

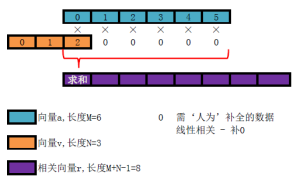
图2. 线性互相关结果序列中单个值计算示意

得到的互相关序列总长度为，该序列的前和后个数值是无效的，有效的数据共个。线性互相关的有效数据第个分量的值为：

注意，线性互相关并不满足交换律，即：

一个简单的应证是，等式两侧操作所得结果的有效数据个数都不一致。

线性相关的实际意义是，向量中的各个与向量等长的子向量与向量的相似程度。这样，中值最大的索引就是与向量中与最相似的子向量的起始索引。通常，为了获得有效的互相关数据，我们总是用较短的数据去滑动点积较长的数据。

用一个实际的应用例子来验证一下吧。如图3的第一个子图表示雷达声纳发射了一个探测信号。经过一段时间之后，收到了如图3的第二个子图所示的回波（带有一定的噪声）。此时我们关注的是如何确定回波中从何时开始是对探测信号的响应，以便计算目标距雷达的距离，这就需要用到线性互相关。在第三个子图中的‘Valid’曲线即是有效互相关数据，其中清晰地呈现出两处与探测信号相似的回波的位置。

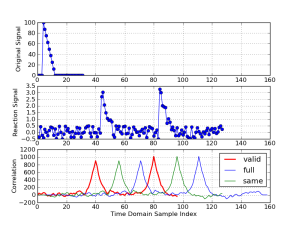
图3. 相关计算的一个例子：雷达回波分析

线性互相关中，还有一些概念值得注意：
一是补零。由线性相关的计算式不难发现，为了计算出个完整的相关系数序列（包含那些“无效数据”在内的所有结果），需要用到一些“不存在”的点。这就需要人为地对这些值进行补充，在线性相关的计算中，对这些超出原始数据储存的区域取值为零。
二是末端效应。由图1可以发现，一头一尾的个互相关数据并没有完全“嵌入”两个原始数组的全部信息，它们或多或少地受到了人为补零的影响。因此一般认为这些数据是不可用的。
三是计算模式的选择。这个问题其实是由问题二衍生而来的，就Python语言中的函数而言，至少有两个可以直接计算线性相关：

1	numpy.correlate(a, v, mode)

和

1	scipy.signal.correlate(a, v, mode)

它们的调用参数完全相同。在调用时有三种模式可供选择，它们计算的内容是相同的，但是返回值长度各不相同：
mode = ‘valid’：只返回有效的那一部分相关数据，共$M-N+1$个；
mode = ‘same’：只返回与 等长的那一部分相关数据，共$N$个；
mode = ‘full’：返回全部相关数据，共$M+N-1$个。
图3的第三个子图展示了这三种模式的计算结果，在那个例子中，‘valid’模式是最合适的。

2. 循环互相关（Circular Cross-Correlation）的定义和计算

循环互相关是表征两组等长的周期性数据之间相似性的操作，其与线性互相关的区别也正由“等长”和“周期性”这个两特点产生。在循环互相关中，被处理的原始数据是等长的，即和。序列和之间的线性互相关操作表示为，其结果也是一个序列，表示为。其计算式与线性互相关的写法是一致的：

只是得到的互相关序列长度也为。循环互相关的计算的具体过程如图4所示，注意到在计算时要用到超出原始数据索引范围的数据，其数据补充方式并不是“补零”而是“周期延拓”：即。这意味着对于循环互相关，不存在不同的计算模式之分，所有的数据都是有效数据。

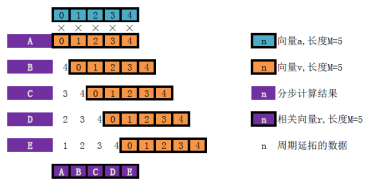
图4. 循环互相关的计算过程示意

注意，循环互相关也不满足交换律。

这里给出了一个关于循环相关的算例。两路原始数据分别由如下函数生成：

如果视为某个线性系统的周期输入信号，而视为这个线性系统的输出信号。由于存在外接干扰，因此输出信号不完全由输入信号决定。此时，循环互相关的实际意义是，分辨输出信号中的哪一个部分（频率成分）是由该输入信号产生的。

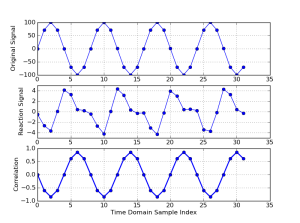
图5. 时域数据，从上到下：，和他们的循环互相关

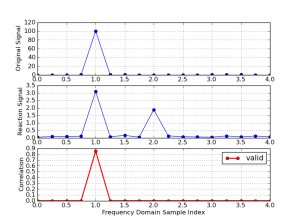
图6. 频谱，从上到下：，和他们的循环互相关

从图5和图6可以看出，循环互相关的频谱准确地说明了那些测试信号的相关性。

遗憾的是，在Python几大数值计算库中，并没有直接可计算循环相关的函数。但是可以采用如下代码构造出一个可用的（经过归一化的）cxcorr(a, v)函数出来：

1 2 3

def cxcorr(a,v): nom = np.linalg.norm(a[:])*np.linalg.norm(v[:]) return fftpack.irfft(fftpack.rfft(a)*fftpack.rfft(v[::-1]))/nom

图4中的数据就是通过这个函数计算出来的。其中用到了傅里叶变换和反变换来计算循环互相关，这是可行的。它们之间的关系在第四小节的QA中专门讨论。

3. 用线性互相关处理周期性信号

实际上，线性相关也可以处理周期信号，前提是将两组信号采样成不长度差异较大的序列。这样，其有效线性互相关也可以完美地反应数据之间的相关性。

同样采用第二节中的例子。这时为了保证足够的有效线性互相关数据，两组数据的长度故意不一致（但都足够表征其特征），如图7所示。它们的频谱如图8所示，仍然完美地体现了测试数据的相关性。

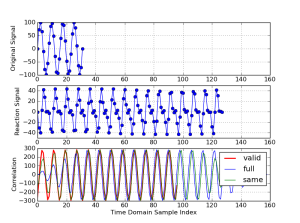
图7. 时域数据，从上到下：，和他们的线性互相关

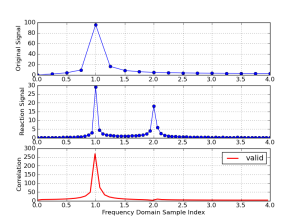
图8. 频谱，从上到下：，和他们的线性互相关

既然线性互相关也能处理周期性数据，为什么还要专门搞一个基于等长序列和周期延拓的循环互相关呢？实际上，正如后文QA中专门讨论的，这是为了利用快速傅利叶变换加速计算。

4. 相关问题QA

至此，两种常用的互相关评价方法及其计算已经总结完毕。然而其中还有一些细节尚待分辨。例如，序列和之间的互相关的计算式：

与卷积（convolution）的定义式：

如此类似，如果再联想起傅里叶变换的卷积定理，那么，至少会产生如下的问题：

Q.1：它们之间有更深意义上的联系吗？
A.1：文献[1]的答复是坚决的：“不要让求卷积和互相关的数学相似性迷惑你，它们描述了不同的信号处理过程。卷积是系统输入信号、输出信号和冲激响应之间的关系。互相关是一种在噪声背景下检测已知信号的方法。二者在数学上的相似仅仅是一种巧合。”实际上，只要注意到卷积操作是满足交换律的，而互相关操作并不满足交换律。仅此一点也许就能说明它们有着本质的不同吧。

Q.2：可以利用Python中计算卷积的函数来计算互相关吗？
A.2：可以，但是只能用以计算线性互相关。Python中的numpy.convolve()函数就可以计算两个序列之间的卷积。在卷积的计算过程中也会自动进行补零（而不是周期延拓，这就是为什么只能计算线性相关的原因），这种卷积有时被称为线性卷积，同样涉及末端效应、有效数据长度等考虑。具体地，根据相关和卷积的表达式，如果希望计算序列和之间的线性互相关序列。等效地，只需要计算序列和之间的卷积。表示序列的“反置”，即将序列[1,2,3]反置为[3,2,1]。

Q.3：可以根据傅立叶变换的性质中有卷积定理，利用傅立叶正/逆变换计算互相关吗？
A.3：可以，但是只能用于计算循环互相关。傅立叶变换的卷积定理中所涉及的卷积是循环卷积。与前述的线性卷积是不同的。实际上不同的并不是卷积本身，它们的计算式是一致的，而是在如何看待参与卷积计算的数据，线性卷积认为参与计算的序列之外都是零，而循环卷积认为参与计算的序列是一个无限循环的数据的一段——这导致了它们对“越界”数据的补齐方式不一样。正如线性互相关和循环互相关的区别！先将循环互相关等效为一个循环卷积，再利用快速傅里叶变换计算卷积即可。实际上本文给出的cxcorr(a, v)函数正是利用这一性质来计算循环相关的。其对计算速度的提升是相当明显的。

Q.4：怎样进行归一化（normalization），以便于比较互相关数据？
A.4：根据参考[4]，用公式：

5. 参考资料

[1] Steven W. Smith. Digital Signal Processing: A Practical Guide for Engineering and Scientists [M].
张瑞峰, 詹敏晶 等译. 实用数字信号处理，从原理到应用[M]. 人民邮电出版社, 北京, 2010.
[2] Mark Owen. Practical Signal Processing [M].
丘天爽, 李丽, 赵林 译. 实用信号处理 [M]. 电子工业出版社, 北京, 2009.
[3] 关于MATLAB中的xcorr() 的论述
http://www.mathworks.cn/cn/help/signal/ref/xcorr.html
[4] 关于MATLAB中的cxcorr() 的论述
http://www.mathworks.com/matlabcentral/fileexchange/4810-circular-cross-correlation
[5] 网络论坛Stackoverflow关于此问题的讨论
http://stackoverflow.com/questions/6991471/computing-cross-correlation-function
http://stackoverflow.com/questions/12323959/fast-cross-correlation-method-in-python
http://stackoverflow.com/questions/9281102/n-fold-fft-convolution-and-circular-overlap
http://stackoverflow.com/questions/6855169/convolution-computations-in-numpy-scipy
http://stackoverflow.com/questions/4688715/find-time-shift-between-two-similar-waveforms
[6] 关于Cross-correlation的定义
http://mathworld.wolfram.com/Cross-Correlation.html
http://paulbourke.net/miscellaneous/correlate/
http://en.wikipedia.org/wiki/Cross-correlation
[7] 关于 Circular Cross-correlation的定义
http://en.wikipedia.org/wiki/Circular_convolution
http://cnx.org/content/m22974/latest/

本文转载自：https://fanyublog.wordpress.com/2015/11/16/corr_python/