二叉树，AVL树和红黑树

为了接下来能更好的学习TreeMap和TreeSet，讲解一下二叉树，AVL树和红黑树。

• 1. 二叉查找树
• 2. AVL树
  • 2.1. 树旋转
    • 2.1.1. 左旋和右旋
    • 2.1.2. 左左，右右，左右，右左
  • 2.2. 删除
• 3. 红黑树
  • 3.1. 插入
  • 3.2. 删除
• 4. 参考文章

1. 二叉查找树

在讲AVL树和红黑树之前，作为铺垫必须先说下二叉树。

二叉树本身不必再说，一棵二叉树称为二叉查找树的条件如下：

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值。
2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值。
3. 任意节点的左、右子树也分别为二叉查找树。
4. 没有键值相等的节点。

通常情况下，采用二叉链表作为二叉树的存储结构。中序遍历二叉树可以得到一个关键字的有序序列，一个无序序列可以通过构造一颗二叉查找树变为有序序列，构造树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。搜索、插入、删除的复杂度等于树高，期望O(log n)，最坏O(n)（数列有序，树退化成线性表）。

通过改进二叉树，保持二叉树的树高为O(log n),可以使二叉树的操作复杂度稳定于O(log n)。因此，产生了AVL树和红黑树。

2. AVL树

AVL树通过树旋转操作实现了维护树高的目的。AVL树中任意节点的两个子树高度差（平衡因子）最大为1，当平衡因子大于1时，该AVL树需要进行树旋转。

2.1. 树旋转

2.1.1. 左旋和右旋

维基上的一个图能够清晰地表述左旋和右旋：

        +---+                          +---+
        | Q |                          | P |
        +---+                          +---+
       /     \     right rotation     /     \
    +---+   +---+  ------------->  +---+   +---+
    | P |   | Z |                  | X |   | Q |
    +---+   +---+  <-------------  +---+   +---+
   /     \          left rotation         /     \
+---+   +---+                          +---+   +---+
| X |   | Y |                          | Y |   | Z |
+---+   +---+                          +---+   +---+

可以看到，左旋的步骤如下:

1. 选择需要旋转的树的新的根节点（图中为Q）。
2. 将选取的节点作为新的根节点，其父节点变为左子节点，其左子节点变为新的左子节点的右子节点。
3. 将新的根节点连接到原根节点的父节点上。

右旋步骤和左旋步骤类似，只是方向相反。左右旋是互逆操作。

2.1.2. 左左，右右，左右，右左

在AVL树中需要树旋转的四种情况旋转方法如下：

• 左左：以中间节点为新的根节点右旋。
• 右右：以中间节点为新的根节点左旋。
• 左右：以最下节点为中心进行一次左旋，变为左左，再以新的中间节点为中心进行一次右旋。
• 右左：以最下节点为中心进行一次右旋，变为右右，再以新的中间节点为中心进行一次左旋。

操作示意如图：

2.2. 删除

从AVL树中删除，可以通过把要删除的节点向下旋转成为一个叶子节点，接着直接移除这个叶子节点。因为旋转成叶子节点期间最多有logn个节点被旋转，因此，AVL删除节点耗费O(logn)时间。

3. 红黑树

红黑树和AVL树一样，都是在查找删除时进行特定操作以维持高性能的特定的平衡二叉树。它可以在O(logn)时间内查找，插入和删除。红黑树相对于普通的二叉树，其性质如下：

1. 红黑树的每个节点都有颜色，为红色（R）或黑色（B），也成RB树。
2. 红黑树的根节点为黑色。
3. 红黑树的每个叶节点（即NIL节点，也叫空节点）为黑色。
4. 每个红色节点的两个子节点都是黑色。（从每个叶子到根的所有节点没有连续的红色）
5. 从任意节点到每个叶子所在的路径都包含相同数目的黑色。

3.1. 插入

插入节点有以下几个关键点：

• 插入节点总是红色节点。
• 如果插入节点的父节点是黑色，能维持性质。
• 如果插入节点的父节点是红色，破坏了性质，要通过旋转或重新着色来维持性质。

插入时，我们按照二叉树的插入来运行，如果我们插入了根节点，由于插入点是红色，则破坏了性质2，如果父节点是红色，则破坏性质4。

因此，插入的伪代码如下：

RB-INSERT(T, z)
y ← nil
x ← T.root
while x ≠ T.nil
    do y ← x
    if z.key < x.key
        then x ← x.left
    else x ← x.right
z.p ← y
if y == nil[T]
    then T.root ← z
else if z.key < y.key
    then y.left ← z
else y.right ← z
z.left ← T.nil
z.right ← T.nil
z.color ← RED
RB-INSERT-FIXUP(T, z)

现在详细解释一下伪代码。考虑各种插入情况和应对方案:

• 插入的是跟节点：原树为空树，违反了性质2。直接涂黑。
• 插入的节点父节点是黑色：未违反任何性质。

以上两种情况比较简单，接下来介绍三种比较复杂的情况。

• 插入的节点的父节点是红色，且祖父节点的另一个节点（叔叔节点）是红色：将当前节点的父节点和叔叔节点变为黑色，祖父节点变为红色，让当前节点指向祖父节点，重新进行判断。下面图片演示了该变化过程。

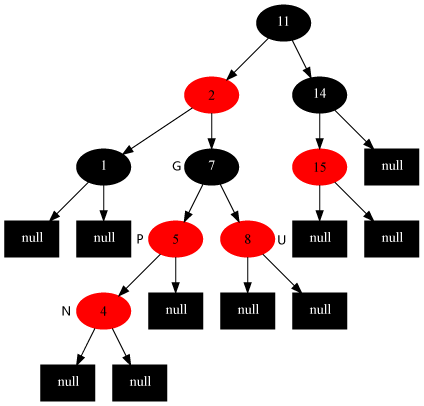
• 插入的节点的父节点是红色，且祖父节点的另一个节点（叔叔节点）是黑色，当前节点是父节点的左（右）子节点同时父节点是祖父节点的右（左）节点：将当前节点的父节点作为新的当前节点，之后，将新当前节点和其子节点即原当前节点部分进行右（左）旋转，此后，重新进行判定。

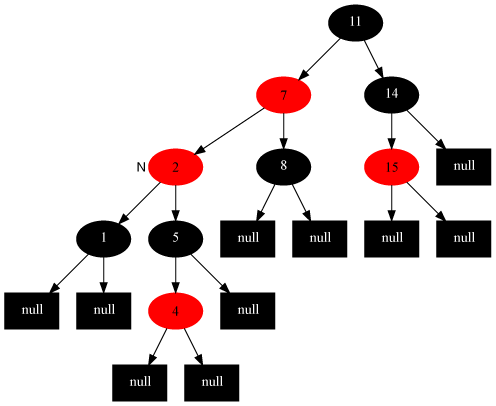
• 插入的节点的父节点是红色，且祖父节点的另一个节点（叔叔节点）是黑色，当前节点是父节点的左（右）子节点同时父节点是祖父节点的左（右）节点：父节点变为黑色，祖父节点变为红色，祖父节点和父节点部分进行右旋。

3.2. 删除

删除的节点的方法与常规二叉搜索树中删除节点的方法是一样的，即，如果它有不足两个非空子节点，则直接用其子节点替代/直接删除。如过它有两个非空子节点，则用左树最大节点/右树最小节点进行替换后进行修复。

和插入类似，删除也有多种情况。伪代码如下：

while x ≠ root[T] and color[x] = BLACK
    do if x = left[p[x]]
          then w ← right[p[x]]
               if color[w] = RED
                  then color[w] ← BLACK                        ▹  Case 1
                       color[p[x]] ← RED                       ▹  Case 1
                       LEFT-ROTATE(T, p[x])                    ▹  Case 1
                       w ← right[p[x]]                         ▹  Case 1
               if color[left[w]] = BLACK and color[right[w]] = BLACK
                  then color[w] ← RED                          ▹  Case 2
                       x ← p[x]                                ▹  Case 2
                  else if color[right[w]] = BLACK
                          then color[left[w]] ← BLACK          ▹  Case 3
                               color[w] ← RED                  ▹  Case 3
                               RIGHT-ROTATE(T, w)              ▹  Case 3
                               w ← right[p[x]]                 ▹  Case 3
                        color[w] ← color[p[x]]                 ▹  Case 4
                        color[p[x]] ← BLACK                    ▹  Case 4
                        color[right[w]] ← BLACK                ▹  Case 4
                        LEFT-ROTATE(T, p[x])                   ▹  Case 4
                        x ← root[T]                            ▹  Case 4
       else (same as then clause with "right" and "left" exchanged)
color[x] ← BLACK  

从伪代码我们可以考虑各种情况。因为该点为替换而来的原叶子节点，所以必为黑色。

• 该点为根节点：什么都不用做。
• 该点的兄弟节点为红色：将兄弟节点染黑，父节点染红，并将二者部分进行左旋（若兄弟节点为左节点则右旋）。
• 该点的兄弟节点为黑色且兄弟节点的两个子节点均为黑色：兄弟节点涂黑，当前节点变为当前节点的父节点，重新判断。
• 该点的兄弟节点为黑色且兄弟节点的左子节点为红色，右子节点为黑色（若兄弟节点为左节点则相反）：兄弟节点左子节点变为黑色，兄弟节点变为红色，将二者进行一次右旋（若兄弟节点为左节点则颜色旋转方向相反）。
• 该点的兄弟节点为黑色且兄弟节点的左子为黑色（若兄弟节点为左节点则为红色）：把兄弟节点颜色染为父节点颜色，父节点颜色和兄弟节点的右子节点（若兄弟节点为左节点则相反）染为黑色，然后将二者进行左旋（兄弟为左节点则右旋），算法结束。

4. 参考文章

AVL树

红黑树

教你初步了解红黑树