【吃炸弹的鸽子UVA10765-双联通模板】

·从前有一个鸽子Lence，它吃了一个炸弹，然后有人出了这道题。

·英文题，述大意：

       给出一张连通无向图，求出：对于每个点，删去这个点（以及它相连的边以后）时，当前图中的连通块数量，这个值作为该点的Lence值。输出根据Lence值从大到小（相同时标号从小到大）的前m个点和它的Lence值。

·分析：

      关于连通块问题，可以寻得三种方法：

      ①嘎嘣脆算法（Gabow）②塔尔杨算法（Tarjan）③Kosaraju算法。

       此处大米饼采用Tarjan算法。

·干什么呢？寻找并标记双连通分量。

在无向图中发现一个双连通分量(这里指边点连通分量)的意义：就算你任意吃掉一个点，这其中的点依然可以互相到达，也就是所谓的连通块。如果我们将一个图划分为多个双联通分量，就是这样：

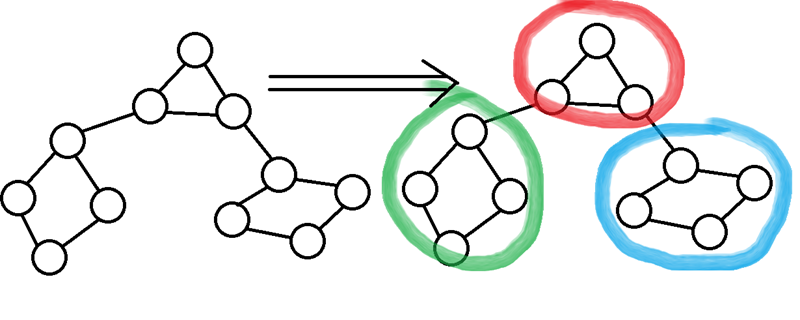
·为了方便观赏，使用缩点操作。就是这样：

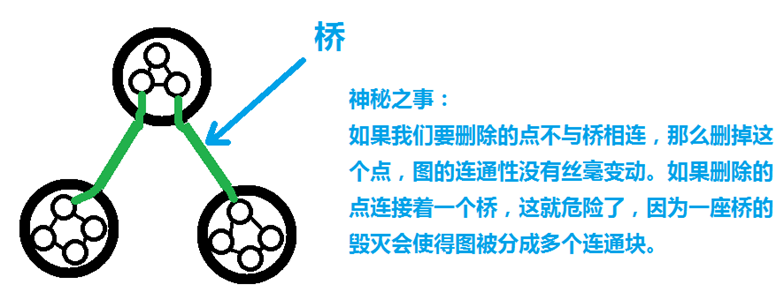
·所以，我们的方法是：根据点的位置进行分类处理。如果这个点不与桥连接，那么整个图还是联通的。如果该点和桥相连，那我们就猜一猜它和几座桥相连（不是猜，认真算！），那么它的毁灭会带来这些桥的毁灭，每一座桥的毁灭会使得一个双联通分量脱离原图，所以：如果这个点连接了num座桥，那么现在这个图就成了风雨飘荡中的(num+1)个部分。

·注意，在实际处理时，我们是用数组记录下每个点连接的桥的个数，所以如果这点不与桥相连，那么就是0，最终答案为0+1=1，因此不需要特殊处理。美妙的模板is drawing closer!

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<cstring>
 4 #define go(i,a,b) for(int i=a;i<=b;i++)
 5 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v)
 6 #define mem(a,b) memset(a,b,sizeof(a))
 7 using namespace std;const int N=10003;
 8 struct E{int v,next;}e[N*100];struct A{int u,val;}ans[N];bool Cut[N];
 9 int n,m,head[N],k,low[N],dfn[N],t,dfs_clock;
10 bool cmp(A a,A b){return a.val==b.val?a.u<b.u:a.val>b.val;}
11 void ADD(int u,int v){e[k]=(E){v,head[u]};head[u]=k++;}
12 void Tarjan(int u,int fa)
13 {
14     low[u]=dfn[u]=++dfs_clock;int num=0,kids=0;
15     fo(i,head,u)if(v!=fa){if(!dfn[v])
16     {
17         kids++;Tarjan(v,u);low[u]=min(low[u],low[v]);
18         if(dfn[u]<=low[v])num++,Cut[u]=1;}//错写成low[u]
19         else low[u]=min(low[u],dfn[v]);
20     }
21     if(!fa&&kids==1)Cut[u]=0,num=0;ans[++t]=(A){u,num};
22 }
23 int main(){while(scanf("%d%d",&n,&m)&&n)
24 {
25     mem(head,0);mem(low,0);mem(dfn,0);mem(Cut,0);t=dfs_clock=0;k=1;int u,v;
26     while(scanf("%d%d",&u,&v)&&++u&&++v)ADD(u,v),ADD(v,u);
27     go(i,1,n)if(!dfn[i])Tarjan(i,0);sort(ans+1,ans+t+1,cmp);
28     go(i,1,m)printf("%d %d\n",ans[i].u-1,ans[i].val+1);
29 puts("");}return 0;}//Paul_Guderian

让我，感到为难的，是挣扎的自由。————赵雷《成都》