Coursera-AndrewNg(吴恩达)机器学习笔记——第一周

一.初识机器学习

1. 何为机器学习？
   A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
   理解：通过实验E，完成某一项任务T，利用评价标准P对实验结果进行迭代优化！
2. 机器学习主要包括监督学习（supervised）和无监督学习（unsupervised），其他的还有增强学习，推荐系统（recommender systems）等。
3. 监督学习是指实验数据当中有可参考的正确输出，通常包括回归问题和分类问题。
4. 回归问题（regression problem）是指预测的值，也就是实验结果是连续的，有准确的数值。
   分类问题（classification problem）是指实验结果是离散的，不是一个准确的数值。
5. 无监督学习指聚类问题，不同于分类。如鸡尾酒会算法，在鸡尾酒会中分辨出人的声音和会场的音乐。

二.单变量线性回归问题（Linear regression with one variable）

1. 符号标记：m（训练集中样本的数量），X`s（输入变量/特征），Y`s（输出变量/目标变量），（x,y）表示一个训练样本。
2. 问题背景：使用房屋面积预测房价！问题描述如下图：
   
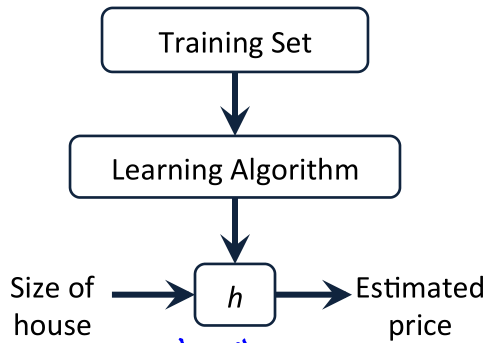
   上图从上向下看，表示将训练集带入到学习算法当中，进过训练得到预测函数h；再从左向右看，将房屋面积带入预测函数，输出预测的房价。
3. 单变量线性回归问题的预测函数可以表示为：h_θ(x)=θ₀+θ₁*x（其实就是y=ax+b），其中的θ_i为模型参数。所以我们的任务就变成了，使用训练集进行训练，最后得到最佳的θ_i值，使得我们得到的预测函数h_θ(x)最接近真正的预测函数。完成此任务的方法就叫做学习算法。
4. 代价函数（cost function）也叫平方误差函数：
   
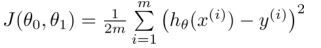
   理解：量化房价预测值h_θ(x⁽ⁱ⁾)和实际房价值y⁽ⁱ⁾之间的偏差。因此，我们每次实验的目标就是通过调整参数θ_i，使得代价函数的值越来越小，这样我们的模型就越接近真实的预测模型。
5. 根据不同的参数θ_i，计算代价函数J(θ₀,θ₁)，作出图形通常称为contour plot（等高线图），图形特点有局部最优解，也就是局部最低点。如下图所示：
   
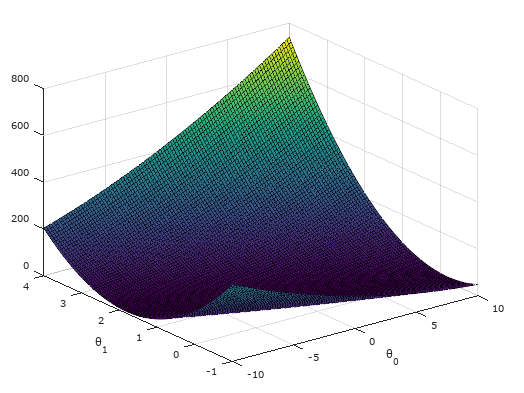
6. 梯度下降（Gradient descent）：通过调整参数θ_i值，不断的降低代价函数J(θ₀,θ₁)，最后找到满意的局部最优解的过程。（参数值需初始化）
   梯度下降算法：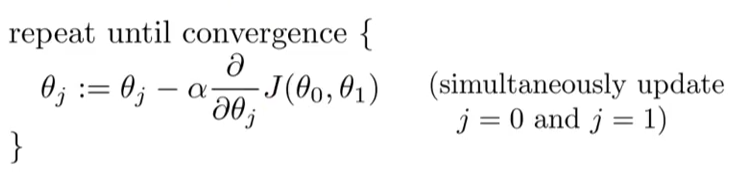
   
   其中α为学习速率，如果α值过小，梯度下降速度慢；如果α过大，梯度下降难以收敛，甚至发散。
7. 单变量线性回归问题的梯度下降形式：
   
   每一次梯度下降计算过程中，都使用训练集中所有的样本！

三.线性代数知识点回顾

1. 矩阵与向量：
   矩阵的维数：m*n（行数*列数）、矩阵中的元素：A_ij（i行j列）、向量是一个n*1维的矩阵、向量中的元素：y_i表示第i个元素。
   通常用大写字母表示矩阵，小写字母表示向量。一般情况下，矩阵和向量的下标索引值从数字1开始。R表示实数集，R_m*n表示m*n维矩阵，矩阵中元素为实数。
   MATLAB/Octive中代码表示：A=[1,2,3;4,5,6;7,8,9;10,11,12]   v=[1;2;3]其中符号;表示开启新行。[m,n]=size(A) 求A的维数m*n，也可写作dim_A=size(A)。同理dim_v=size(v)。A_23=A(2,3)表示取2行3列的值。
2. 矩阵的加减法：只有两个相同维度的矩阵才可以进行加减法。
                        
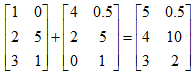
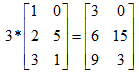
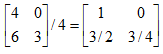
3. 矩阵乘法不满足交换律A*B!=B*A，但是满足结合律A*B*C=A*(B*C)
   
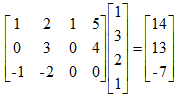
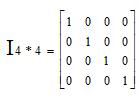
   I为单位矩阵，A*I=I*A=A.
4. 矩阵的逆：AA^-1=A^-1A=I，其中A为m*m维的方阵，只有方阵才有逆矩阵。
   矩阵的转置：A_m*n，B=A^T，B_n*m，and B_ij=A_ij