digital root问题
问题阐述会是这样的:
Given a non-negative integer num, repeatedly add all its digits until the result has only one digit.
For example:
Given num = 38, the process is like: 3 + 8 = 11, 1 + 1 = 2. Since 2 has only one digit, return it.
Follow up:
Could you do it without any loop/recursion in O(1) runtime?
这其实是一个digital root的问题。
digital root的定义如下:
The digital root (also repeated digital sum) of a non-negative integer is the (single digit) value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum. The process continues until a single-digit number is reached.
For example, the digital root of 65,536 is 7, because 6 + 5 + 5 + 3 + 6 = 25 and 2 + 5 = 7.
编程题中一般会要求在O(1)时间算出一个数的digital root,这时候就不能用上述思想解答问题了。
通用公式:
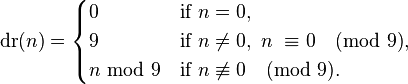 或者是
或者是
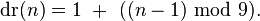
所有的原理其实和模运算以及同余定理有关:
考虑12345 = 1 × 10,000 + 2 × 1,000 + 3 × 100 + 4 × 10 + 5.
同时10 i= 9 + 1; 100 i= 99 + 1,所以又可以写成:
12,345 = 1 × (9,999 + 1) + 2 × (999 + 1) + 3 × (99 + 1) + 4 × (9 + 1) + 5.
展开后:
12,345 = (1 × 9,999 + 2 × 999 + 3 × 99 + 4 × 9) + (1 + 2 + 3 + 4 + 5).
这样便满足了数根的思想,计算数根的一次迭代,当然(1 + 2 + 3 + 4 + 5)=15 又可以接着迭代,总之是:

数根是模9的余数是因为 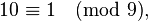 因此
因此 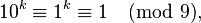 这样便有
这样便有 ,也就有如下推论:
,也就有如下推论:

这里要强调为什么当数字是9的倍数时,dr(n)是9?
例如:18 = 10 + 9
$18 \equiv 0 \pmod{9}$
但 $10 + 9 \equiv 1 + 8 \pmod{9}$,莫着急,这只是表象, $1 + 8 = 9 \equiv 0 \pmod{9}$
所以9的倍数的数根也可以用(mod 9)运算,只不过由于数根只在1-9之间,所以为零时只要换成9即可,毕竟$9 \equiv 0 \pmod{9}$
至于
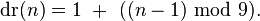 也是这个道理,数根只能在1-9之间,而(mod 9)的数域在0-8之间, 所以先对数字减1然后再补1即可折中等效了。
也是这个道理,数根只能在1-9之间,而(mod 9)的数域在0-8之间, 所以先对数字减1然后再补1即可折中等效了。
关键点是理解为什么由
$a = b + c$
$b \equiv r_1 \pmod{9} $
$c \equiv r_2 \pmod{9} $
可推导出:
$a \equiv r_1 + r_2\pmod{9}$
提示:把数写成 $n = mq + r $,依据一条推论:
推论 a≡b(mod m)的充要条件是a=mt+b(t为整数)。
表示对模m同余关系的式子叫做模m的同余式,简称同余。
参考资料:
A NEAT NUMBER TRICK: DIGITAL ROOTS AND MODULO-9 ARITHMETIC
digital root问题的更多相关文章
- Digital root(数根)
关于digital root可以参考维基百科,这里给出基本定义和性质. 一.定义 数字根(Digital Root)就是把一个数的各位数字相加,再将所得数的各位数字相加,直到所得数为一位数字为止.而这 ...
- 数字根(digital root)
来源:LeetCode 258 Add Dights Question:Given a non-negative integer num , repeatedly add all its digi ...
- 【HDOJ】4351 Digital root
digital root = n==0 ? 0 : n%9==0 ? 9:n%9;可以简单证明一下n = a0*n^0 + a1*n^1 + ... + ak * n^kn%9 = a0+a1+..+ ...
- Sum of Digits / Digital Root
Sum of Digits / Digital Root In this kata, you must create a digital root function. A digital root i ...
- 1. 数字根(Digital Root)
数字根(Digital Root)就是把一个自然数的各位数字相加,再将所得数的各位数字相加,直到所得数为一位数字为止.而这个一位数便是原来数字的数字根.例如: 198的数字根为9(1+9+8=18,1 ...
- 快速切题 sgu118. Digital Root 秦九韶公式
118. Digital Root time limit per test: 0.25 sec. memory limit per test: 4096 KB Let f(n) be a sum of ...
- Codeforces Beta Round #10 C. Digital Root 数学
C. Digital Root 题目连接: http://www.codeforces.com/contest/10/problem/C Description Not long ago Billy ...
- 数学 - SGU 118. Digital Root
Digital Root Problem's Link Mean: 定义f(n)为n各位数字之和,如果n是各位数,则n个数根是f(n),否则为f(n)的数根. 现在给出n个Ai,求出A1*A2*…*A ...
- 构造水题 Codeforces Round #206 (Div. 2) A. Vasya and Digital Root
题目传送门 /* 构造水题:对于0的多个位数的NO,对于位数太大的在后面补0,在9×k的范围内的平均的原则 */ #include <cstdio> #include <algori ...
随机推荐
- 【转】关于C++程序的编码问题
引用自:http://blog.chinaunix.net/uid-26790551-id-3190813.html 我们传统的程序基本都只在Windows或只在Linux下运行,Windows程序使 ...
- web.xml中<load-on-start>n</load-on-satrt>作用
如下面一段配置,我们再熟悉不过了: 我们注意到它里面包含了这段配置:<load-on-startup>1</load-on-startup>,那么这个配置有什么作用呢? 作用如 ...
- JSON之三:获取JSON文本并解释(以google的天气API为例)
google提供了天气的api,以广州天气为例,地址为: http://api.openweathermap.org/data/2.5/weather?q=guangzhou 返回的结果为: { ...
- java压缩/解压缩zip格式文件
因为项目要用到压缩.解压缩zip格式压缩包,只好自己封装一个,对于网上流行的中文乱码的问题,本文的解决方法是用apache的包代替jdk里的.基本上还是比较好用的. 废话少说,直接上代码. } ...
- php 记住密码自动登录
当我们登录网站管理后台的时候,会有提示说记住登录状态,记住我等这样的提示,这个选项有什么用呢?如果选中了记登录状态后,下次在浏览这个网站后 台时就不用在填写用户名和密码了,在去登录了.下面写了一小代码 ...
- phpStudy速度慢的解决办法
1.修改mysql数据库链接地址为ip地址127.0.0.1. 2.使用最新版本,这个坑了我好久时间.
- java性能优化技巧
在JAVA程序中,性能问题的大部分原因并不在于JAVA语言,而是程序本身.养成良好的编码习惯非常重要,能够显著地提升程序性能. 1. 尽量使用final修饰符. 带有final修饰符的类是不可派生的. ...
- Swift笔记4
字符 var str = " hello world " var kong = "" 或者 var kong = string() //定义一个空的字符 ...
- entity framework如何控制并发
entity framework如何控制并发 针对字段http://msdn.microsoft.com/en-us/library/vstudio/bb738618(v=vs.100).aspx ...
- #include <bitset>
1 none();测试是否有越位 2 reset();全部清零 3 set(7, 0);把第7个字符改成0,操作二进制位 4 to_string();转换为字符串 5 to_ulong();转换为无符 ...
