HDU 5531 Rebuild (2015长春现场赛，计算几何+三分法)

Rebuild

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 521    Accepted Submission(s): 125

Problem Description

Archaeologists find ruins of Ancient ACM Civilization, and they want to rebuild it.

The ruins form a closed path on an x-y plane, which has n endpoints. The endpoints locate on (x1,y1), (x2,y2), …,(xn,yn) respectively. Endpoint i and endpointi−1 are adjacent for 1<i≤n, also endpoint 1 and endpoint n are adjacent. Distances between any two adjacent endpoints are positive integers.

To rebuild, they need to build one cylindrical pillar at each endpoint, the radius of the pillar of endpoint i is ri. All the pillars perpendicular to the x-y plane, and the corresponding endpoint is on the centerline of it. We call two pillars are adjacent if and only if two corresponding endpoints are adjacent. For any two adjacent pillars, one must be tangent externally to another, otherwise it will violate the aesthetics of Ancient ACM Civilization. If two pillars are not adjacent, then there are no constraints, even if they overlap each other.

Note that ri must not be less than 0 since we cannot build a pillar with negative radius and pillars with zero radius are acceptable since those kind of pillars still exist in their neighbors.

You are given the coordinates of n endpoints. Your task is to find r1,r2,…,rn which makes sum of base area of all pillars as minimum as possible.

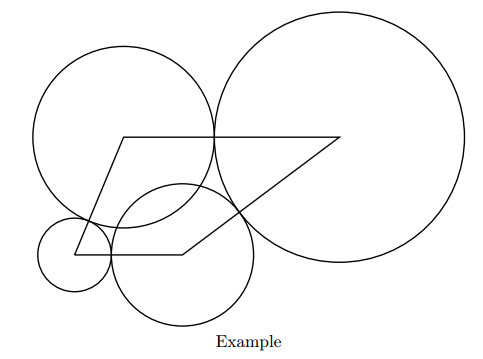
For example, if the endpoints are at (0,0), (11,0), (27,12), (5,12), we can choose (r1, r2, r3, r4)=(3.75, 7.25, 12.75, 9.25). The sum of base area equals to 3.752π+7.252π+12.752π+9.252π=988.816…. Note that we count the area of the overlapping parts multiple times.

If there are several possible to produce the minimum sum of base area, you may output any of them.

 

Input

The first line contains an integer t indicating the total number of test cases. The following lines describe a test case.

The first line of each case contains one positive integer n, the size of the closed path. Next n lines, each line consists of two integers (xi,yi) indicate the coordinate of the i-th endpoint.

1≤t≤100
3≤n≤104
|xi|,|yi|≤104
Distances between any two adjacent endpoints are positive integers.

 

Output

If such answer doesn't exist, then print on a single line "IMPOSSIBLE" (without the quotes). Otherwise, in the first line print the minimum sum of base area, and then print n lines, the i-th of them should contain a number ri, rounded to 2 digits after the decimal point.

If there are several possible ways to produce the minimum sum of base area, you may output any of them.

 

Sample Input

3
4
0 0
11 0
27 12
5 12
5
0 0
7 0
7 3
3 6
0 6
5
0 0
1 0
6 12
3 16
0 12

 

Sample Output

988.82
3.75
7.25
12.75
9.25
157.08
6.00
1.00
2.00
3.00
0.00
IMPOSSIBLE

 

Source

2015ACM/ICPC亚洲区长春站-重现赛（感谢东北师大）

 

 

 

【题意】：

给出一个Ｎ边形的顶点和边长，对于每个顶点作一圆，要求邻接顶点对应的两圆外切（不相邻顶点无要求）。找出一组Ｒi（Ｒ＞＝０）使得所有圆的面积和最小。

【解题思路】：

由于邻接点对应的圆要外切，则确定一个圆的半径ｒ后，即可唯一确定所有圆的半径（Ri = di - Ri-1）；设连接点 1 与 n 的边为 d1，以此类推。则必须满足 R1 + Rn = d1。根据此关系可以得到一个关于r与d的等式。

化简容易看出：

①当 n 为奇数时，可行的 r 可以唯一确定，r = d1+ （d2+…+d(2n)) - (d3+…+d(2n+1));

②当 n 为偶数时，必定满足 d1+d3+d5+… = d2+d4+d6+…，否则IMPOSSIBLE（仅为必要条件）

此时 S = r1^2 + … +rn^2  = ax^2+bx+c 为一个二次函数表达式。

用 r 来表示Ri，首先可计算出a b c. 再根据每 ri <= di 这个关系求出r的取值范围[low, high].（无范围则IMPOSSIBLE）

有了二次函数表达式和自变量范围，用三分法求出半径平方和取最小值时的 r .

根据①②求出的 r ，计算出所有的Ri，再依次判断每个Ri是否非负。

注意精度问题（坑点！）：

由于本题只保留2位小数，计算面积和时，若用 S = Sum（pi*r*r）计算则会出现精度问题（具体解释不清、亲测会挂），须在括号外乘PI，即 S = pi * Sum（r*r）.

现场这题过得不多，封榜时一口气打完交了2发WA，当时感觉思路非常清晰正确，不知道从哪调起，不停换机位到最后也没过。

当时怨念很深，把代码打印带了回来查个究竟。先是在某论坛看到有人说精度这个坑，后来HDU重现赛再打，发现一个重大且傻逼的错误，当时求出二次函数后，以为最低点(-b/2a)如果取不到则IMPOSSIBLE当时想了三分以为跟这个是一样的），但显然要根据 r 的取值范围用三分法来逼近最小值。

长春打铁很遗憾，第一次参加 ICPC 区域赛，既有遗憾也有教训。归根结底还是自己太弱，而且还不好好训练。明年就大三了，有了这次教训，接下来一年一定要好好训练好好总结，争取早日取得成绩。同时，stark 目前也还有各方面欠缺，希望能跟队友共勉，一起努力。

Upd 15.11.6 合肥赛前总结下长春得失，希望合肥站加油！(默默感谢队友wqp让出这个机会).

 

 

 

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #define eps 1e-8
 #define PI acos(-1.0)
 #define LL long long
 #define maxn 100100
 #define IN freopen("in.txt","r",stdin);
 using namespace std;

 struct Point {
     double x,y;
 };

 int sign(double x) {
     if(fabs(x)<eps) return ;
     return x<? -:;
 }

 double Distance(Point p1,Point p2) {
     return sqrt((p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y));
 }

 int n;
 Point p[maxn];
 double d[maxn];

 int check(double r)
 {
     if(sign(r) < ) return ;

     for(int i= ;i<=n; i++) {
         r = d[i]-r;
         if(sign(r) < ) return ;
     }
     return ;
 }

 /*三分法求面积最小时的r*/
 double a,b,c;
 double cal(double x) {
     return a*x*x + b*x + c;
 }

 double solve(double low, double high)
 {
     while(high-low > eps){
         double mid = (high+low)/2.0;
         double midmid = (mid+high)/2.0;
         if(sign(cal(midmid)-cal(mid)) > ) high = midmid;
         else low = mid;
     }

     return low;
 }

 int main(int argc, char const *argv[])
 {
     //IN;

     int t;scanf("%d",&t);
     while(t--)
     {
         double r = ;
         memset(p, , sizeof(p));
         memset(d, , sizeof(d));
         int flag = ;

         scanf("%d", &n);
         for(int i= ;i<=n; i++)
             scanf("%lf %lf", &p[i].x, &p[i].y);
         d[]=Distance(p[], p[n]);
         for(int i=; i<=n; i++)
             d[i] = Distance(p[i], p[i-]);

         if(n% != ){
             r = d[];
             for(int i=; i<=n; i++){
                 if(i% == ) r += d[i];
                 else r -= d[i];
             }
             r /= 2.0;
             flag = check(r);
         }

         else{
             double tmp = ;
             for(int i=; i<=n; i++){
                 if(i% != ) tmp += d[i];
                 else tmp -= d[i];
             }
             if(sign(tmp) != ) {flag=; goto end;}

             /*半径平方和的二次表达式*/
             a=1.0; b=; c=;
             tmp = ;
             for(int i=; i<=n; i++){
                 a += 1.0;
                 tmp = d[i]-tmp;
                 c += tmp*tmp;
                 if(i% == ) b -= 2.0*tmp;
                 else b += 2.0*tmp;
             }

             /*
                 错误地以为最低点为唯一取值点,若最低点不符合则无解.
                 r=(-b)/(2.0*a);
                 if(sign(r)<0) r=0;
                 flag = check(r);
             */

             /*检查每条边计算三分时r的可行范围*/
             double low=, high = d[];
             tmp = ;
             for(int i=; i<=n; i++){
                 if(i% == ){
                     tmp += d[i];
                     high = min(high, tmp);
                 }
                 else{
                     tmp -= d[i];
                     low = max(low, tmp);
                 }
             }

             if(low > high) flag = ;
             else{
                 r = solve(low, high);
                 flag = check(r);
             }
         }

         end:
         if(!flag) printf("IMPOSSIBLE\n");
         else{
             double R[maxn];
             R[]=r;
             double temp = ;
             for(int i=; i<=n; i++){
                 temp = d[i]-R[i-];
                 R[i] = temp;
             }
             double ans = ;
             for(int i=; i<=n; i++){
                 //ans += R[i]*R[i]*PI;精度问题
                 ans += R[i]*R[i];
             }

             printf("%.2lf\n", ans*PI);
             for(int i=; i<=n; i++){
                 printf("%.2lf\n", R[i]);
             }
         }

     }

     return ;
 }