A*算法解决八数码问题 Java语言实现

0X00　　定义

　　首先要明确一下什么是A*算法和八数码问题？

　　A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法也是一种启发性的算法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。启发中的估价是用估价函数表示的，如：

f(n) = g(n) + h(n) 

其中f(n) 是节点n的估价函数，g(n)实在状态空间中从初始节点到n节点的实际代价，h(n)是从n到目 标节点最佳路径的估计代价。其中最重要的是h(n)函数，要求

h(n)<h'(n) 

其中h'(n)为实际中当前状态要到达目标状态的步骤数。

　　八数码问题就是在一个3*3的矩阵中摆放1-8一共八个数字，还有一个空余的位置用于移动来改变当前的位置来达到最终的状态。如下图

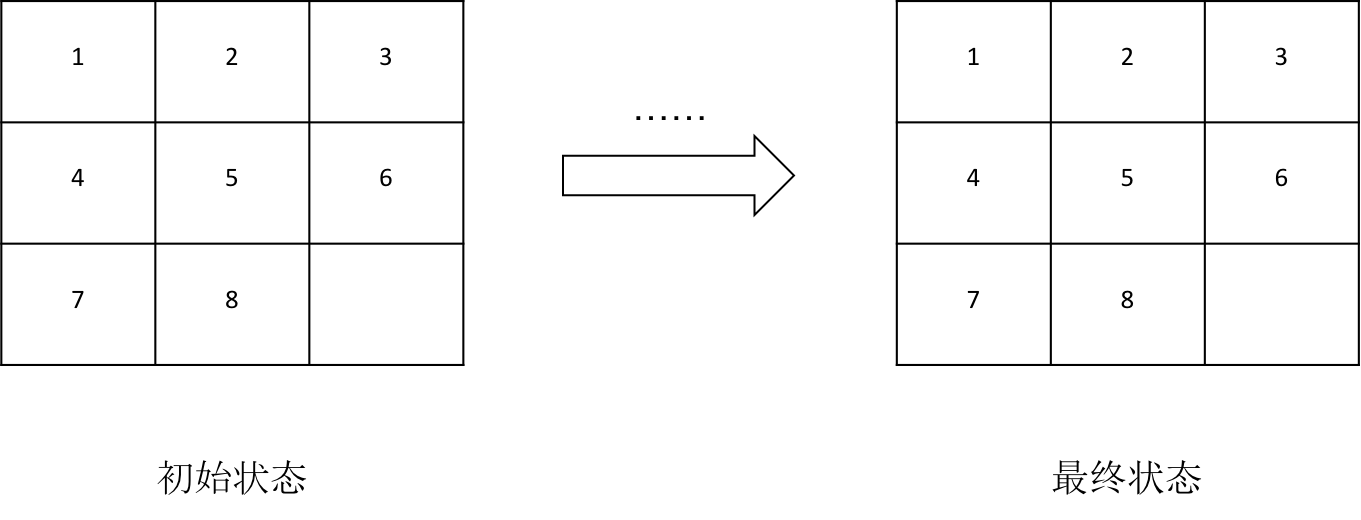
0X01　　分析八数码问题

　　首先我们要简化一下八数码问题，我们移动数字就是相当于移动空格。这样我们就将问题简化为空格的移动，空格移动的状态只有4种：上、下、左、右。然而在八数码问题中并不是每次空格的移动都有四种状态，我们要判断在当前位置也移动的状态才能移动，我们还要去掉一种状态就是当前状态的父状态，因为如果我们移动到父状态则相当于回退了一步。

　　然后，我们要关心的就是给定的初始化状态是否能够通过移动而达到目标状态。这就涉及到了数学问题，就是如果初始状态和目标状态的逆序值同为奇数或同为偶数则可以通过有限次数的移动到达目标状态，否则无解。

　　既然我们已经清楚了空格移动的方式，我们讨论一下空格的几种移动的可能方式：

对应的状态如图所示。

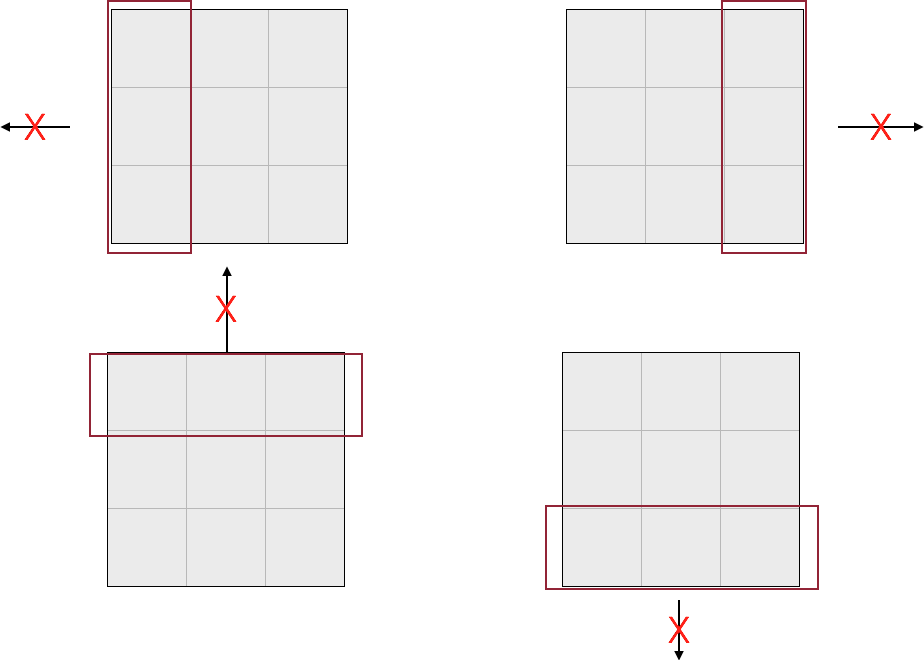
0X02 算法的实现

　　A*算法的实现有一个具体的流程图：

　

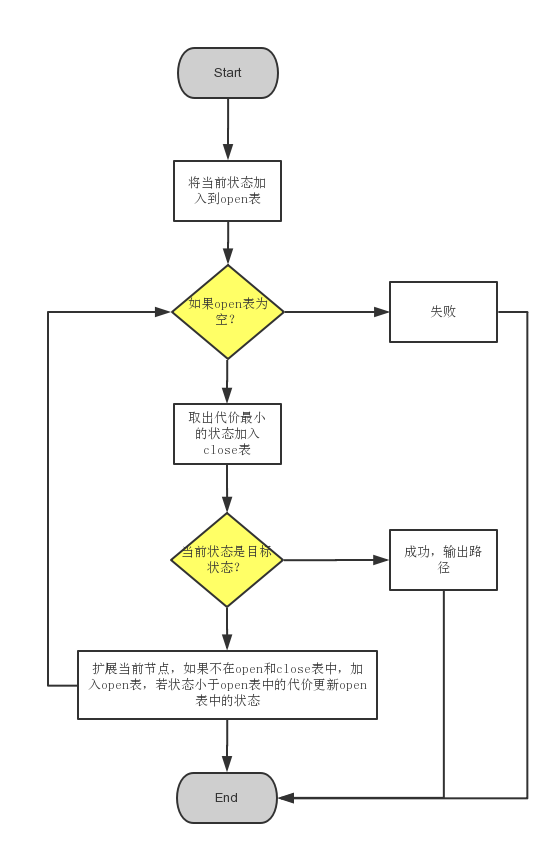
我们使用A*来解决八数码问题，首先我们定义一下f(n),g(n)和h(n)。

　　f(n):估计从初始状态到目标状态的代价。

　　g(n):从初始状态到当前状态的实际代价。

　　h(n):当前状态与目标状态的错位数。

首先我们定义八数码一个状态中的属性：

 　　 private int[] num = new int[9];
     private int depth;                    //当前的深度即走到当前状态的步骤
     private int evaluation;                //从起始状态到目标的最小估计值
     private int misposition;            //到目标的最小估计
     private EightPuzzle parent;            //当前状态的父状态

然后定义状态初始化信息：

          /**
      * 求f(n) = g(n)+h(n);
      * 初始化状态信息
      * @param target
      */
     public void init(EightPuzzle target){
         int temp = 0;
         for(int i=0;i<9;i++){
             if(num[i]!=target.getNum()[i])
                 temp++;
         }
         this.setMisposition(temp);
         if(this.getParent()==null){
             this.setDepth(0);
         }else{
             this.depth = this.parent.getDepth()+1;
         }
         this.setEvaluation(this.getDepth()+this.getMisposition());
     }            

如果能够找到目标状态，将会通过parent属相找到路径并输出。

0X03 代码实现

 import java.io.BufferedReader;
 import java.io.FileNotFoundException;
 import java.io.FileReader;
 import java.io.IOException;
 import java.util.ArrayList;
 import java.util.Arrays;
 import java.util.Collections;
 import java.util.Scanner;

 @SuppressWarnings("rawtypes")
 public class EightPuzzle implements Comparable{
     private int[] num = new int[9];
     private int depth;                    //当前的深度即走到当前状态的步骤
     private int evaluation;                //从起始状态到目标的最小估计值
     private int misposition;            //到目标的最小估计
     private EightPuzzle parent;            //当前状态的父状态
     public int[] getNum() {
         return num;
     }
     public void setNum(int[] num) {
         this.num = num;
     }
     public int getDepth() {
         return depth;
     }
     public void setDepth(int depth) {
         this.depth = depth;
     }
     public int getEvaluation() {
         return evaluation;
     }
     public void setEvaluation(int evaluation) {
         this.evaluation = evaluation;
     }
     public int getMisposition() {
         return misposition;
     }
     public void setMisposition(int misposition) {
         this.misposition = misposition;
     }
     public EightPuzzle getParent() {
         return parent;
     }
     public void setParent(EightPuzzle parent) {
         this.parent = parent;
     }

     /**
      * 判断当前状态是否为目标状态
      * @param target
      * @return
      */
     public boolean isTarget(EightPuzzle target){
         return Arrays.equals(getNum(), target.getNum());
     }

     /**
      * 求f(n) = g(n)+h(n);
      * 初始化状态信息
      * @param target
      */
     public void init(EightPuzzle target){
         int temp = 0;
         for(int i=0;i<9;i++){
             if(num[i]!=target.getNum()[i])
                 temp++;
         }
         this.setMisposition(temp);
         if(this.getParent()==null){
             this.setDepth(0);
         }else{
             this.depth = this.parent.getDepth()+1;
         }
         this.setEvaluation(this.getDepth()+this.getMisposition());
     }

     /**
      * 求逆序值并判断是否有解
      * @param target
      * @return 有解：true 无解：false
      */
     public boolean isSolvable(EightPuzzle target){
         int reverse = 0;
         for(int i=0;i<9;i++){
             for(int j=0;j<i;j++){
                 if(num[j]>num[i])
                     reverse++;
                 if(target.getNum()[j]>target.getNum()[i])
                     reverse++;
             }
         }
         if(reverse % 2 == 0)
             return true;
         return false;
     }
     @Override
     public int compareTo(Object o) {
         EightPuzzle c = (EightPuzzle) o;
         return this.evaluation-c.getEvaluation();//默认排序为f(n)由小到大排序
     }
     /**
      * @return 返回0在八数码中的位置
      */
     public int getZeroPosition(){
         int position = -1;
         for(int i=0;i<9;i++){
             if(this.num[i] == 0){
                 position = i;
             }
         }
         return position;
     }
     /**
      *
      * @param open    状态集合
      * @return 判断当前状态是否存在于open表中
      */
     public int isContains(ArrayList<EightPuzzle> open){
         for(int i=0;i<open.size();i++){
             if(Arrays.equals(open.get(i).getNum(), getNum())){
                 return i;
             }
         }
         return -1;
     }
     /**
      *
      * @return 小于3的不能上移返回false
      */
     public boolean isMoveUp() {
         int position = getZeroPosition();
         if(position<=2){
             return false;
         }
         return true;
     }
     /**
      *
      * @return 大于6返回false
      */
     public boolean isMoveDown() {
         int position = getZeroPosition();
         if(position>=6){
             return false;
         }
         return true;
     }
     /**
      *
      * @return 0，3，6返回false
      */
     public boolean isMoveLeft() {
         int position = getZeroPosition();
         if(position%3 == 0){
             return false;
         }
         return true;
     }
     /**
      *
      * @return 2，5，8不能右移返回false
      */
     public boolean isMoveRight() {
         int position = getZeroPosition();
         if((position)%3 == 2){
             return false;
         }
         return true;
     }
     /**
      *
      * @param move 0：上，1：下，2：左，3：右
      * @return 返回移动后的状态
      */
     public EightPuzzle moveUp(int move){
         EightPuzzle temp = new EightPuzzle();
         int[] tempnum = (int[])num.clone();
         temp.setNum(tempnum);
         int position = getZeroPosition();    //0的位置
         int p=0;                            //与0换位置的位置
         switch(move){
             case 0:
                 p = position-3;
                 temp.getNum()[position] = num[p];
                 break;
             case 1:
                 p = position+3;
                 temp.getNum()[position] = num[p];
                 break;
             case 2:
                 p = position-1;
                 temp.getNum()[position] = num[p];
                 break;
             case 3:
                 p = position+1;
                 temp.getNum()[position] = num[p];
                 break;
         }
         temp.getNum()[p] = 0;
         return temp;
     }
     /**
      * 按照八数码的格式输出
      */
     public void print(){
         for(int i=0;i<9;i++){
             if(i%3 == 2){
                 System.out.println(this.num[i]);
             }else{
                 System.out.print(this.num[i]+"  ");
             }
         }
     }
     /**
      * 反序列的输出状态
      */
     public void printRoute(){
         EightPuzzle temp = null;
         int count = 0;
         temp = this;
         while(temp!=null){
             temp.print();
             System.out.println("----------分割线----------");
             temp = temp.getParent();
             count++;
         }
         System.out.println("步骤数："+(count-1));
     }
     /**
      *
      * @param open open表
      * @param close close表
      * @param parent 父状态
      * @param target 目标状态
      */
     public void operation(ArrayList<EightPuzzle> open,ArrayList<EightPuzzle> close,EightPuzzle parent,EightPuzzle target){
         if(this.isContains(close) == -1){
             int position = this.isContains(open);
             if(position == -1){
                 this.parent = parent;
                 this.init(target);
                 open.add(this);
             }else{
                 if(this.getDepth() < open.get(position).getDepth()){
                     open.remove(position);
                     this.parent = parent;
                     this.init(target);
                     open.add(this);
                 }
             }
         }
     }

     @SuppressWarnings("unchecked")
     public static void main(String args[]){
         //定义open表
         ArrayList<EightPuzzle> open = new ArrayList<EightPuzzle>();
         ArrayList<EightPuzzle> close = new ArrayList<EightPuzzle>();
         EightPuzzle start = new EightPuzzle();
         EightPuzzle target = new EightPuzzle();

         //BufferedReader br = new BufferedReader(new FileReader("./input.txt") );
         String lineContent = null;
         int stnum[] = {2,1,6,4,0,8,7,5,3};
         int tanum[] = {1,2,3,8,0,4,7,6,5};
         int order = 0;
         try {
             BufferedReader br;
             br = new BufferedReader(new FileReader("input.txt") );
             while((lineContent=br.readLine())!=null){
                 String[] str = lineContent.split(",");
                 for(int i = 0 ;i<str.length;i++){
                     if(order==0)
                         stnum[i] = Integer.parseInt(str[i]);
                     else
                         tanum[i] = Integer.parseInt(str[i]);
                 }
                 order++;
             }
         } catch (NumberFormatException e) {
             System.out.println("请检查输入文件的格式，例如：2,1,6,4,0,8,7,5,3 换行 1,2,3,8,0,4,7,6,5");
             e.printStackTrace();
         } catch (IOException e) {
             System.out.println("当前目录下无input.txt文件。");
             e.printStackTrace();
         }
         start.setNum(stnum);
         target.setNum(tanum);
         long startTime=System.currentTimeMillis();   //获取开始时间
         if(start.isSolvable(target)){
             //初始化初始状态
             start.init(target);
             open.add(start);
             while(open.isEmpty() == false){
                 Collections.sort(open);            //按照evaluation的值排序
                 EightPuzzle best = open.get(0);    //从open表中取出最小估值的状态并移除open表
                 open.remove(0);
                 close.add(best);
                 if(best.isTarget(target)){
                     //输出
                     best.printRoute();
                     long end=System.currentTimeMillis(); //获取结束时间
                     System.out.println("程序运行时间： "+(end-startTime)+"ms");
                     System.exit(0);
                 }
                 int move;
                 //由best状态进行扩展并加入到open表中
                 //0的位置上移之后状态不在close和open中设定best为其父状态，并初始化f(n)估值函数
                 if(best.isMoveUp()){
                     move = 0;
                     EightPuzzle up = best.moveUp(move);
                     up.operation(open, close, best, target);
                 }
                 //0的位置下移之后状态不在close和open中设定best为其父状态，并初始化f(n)估值函数
                 if(best.isMoveDown()){
                     move = 1;
                     EightPuzzle up = best.moveUp(move);
                     up.operation(open, close, best, target);
                 }
                 //0的位置左移之后状态不在close和open中设定best为其父状态，并初始化f(n)估值函数
                 if(best.isMoveLeft()){
                     move = 2;
                     EightPuzzle up = best.moveUp(move);
                     up.operation(open, close, best, target);
                 }
                 //0的位置右移之后状态不在close和open中设定best为其父状态，并初始化f(n)估值函数
                 if(best.isMoveRight()){
                     move = 3;
                     EightPuzzle up = best.moveUp(move);
                     up.operation(open, close, best, target);
                 }

             }
         }else
             System.out.println("没有解，请重新输入。");
     }

 }