基于SVD的图像压缩

算法简介

算法实现

我只是简单处理了一下图像的灰度值，如果要处理RGB值的话，就需要分别进行SVD分解，最后再合起来即可。

 import numpy as np
 from PIL import Image
 import matplotlib.pyplot as plt

 def picture_processing(file):  # 图像处理，返回灰度值
     im = Image.open(file)
     im = im.convert('L')   # 转换为灰度图
     #im.save('original_' + file)  # 保存图片
     w, h = im.size
     data = np.zeros((h, w))
     for i in range(w):     # 得到灰度值矩阵
         for j in range(h):
             data[j][i] = im.getpixel((i, j))
     return data

 def picture_restore(U, Sigma, VT, k):   # 图像恢复，k为选取的奇异值个数
     sig = np.eye(k) * Sigma[:k]
     new_pic = U[:, :k].dot(sig).dot(VT[:k, :])   # 重构图片
     new_size = U.shape[0] * k + sig.size + k * VT.shape[1]  # 计算SVD图片所需大小
     #new_im = Image.fromarray(new_pic.astype(np.uint8))  # 保存图片
     #new_im.save('pic_' + str(k) + '.jpeg')
     return new_pic, new_size

 if __name__ == '__main__':
     file = 'pic.jpeg'
     data = picture_processing(file)
     U, Sigma, VT = np.linalg.svd(data)

     pic_list, size_list = [], []   #图片列表，图片大小列表
     k_list = [1, 10, 50, 100, 300]
     for k in k_list:
         new_pic, new_size = picture_restore(U, Sigma, VT, k)
         pic_list.append(new_pic)
         size_list.append(new_size)

     fig, ax = plt.subplots(2, 3)   # 展示
     ax[0][0].imshow(data)
     ax[0][0].set_title('original picture——size:%d' % data.size)
     for i in range(len(k_list)):
         ax[int((i+1) / 3)][int((i+1) % 3)].imshow(pic_list[i])
         ax[int((i+1) / 3)][int((i+1) % 3)].set_title('k = %d——size:%d' % (k_list[i], size_list[i]))
     plt.show()

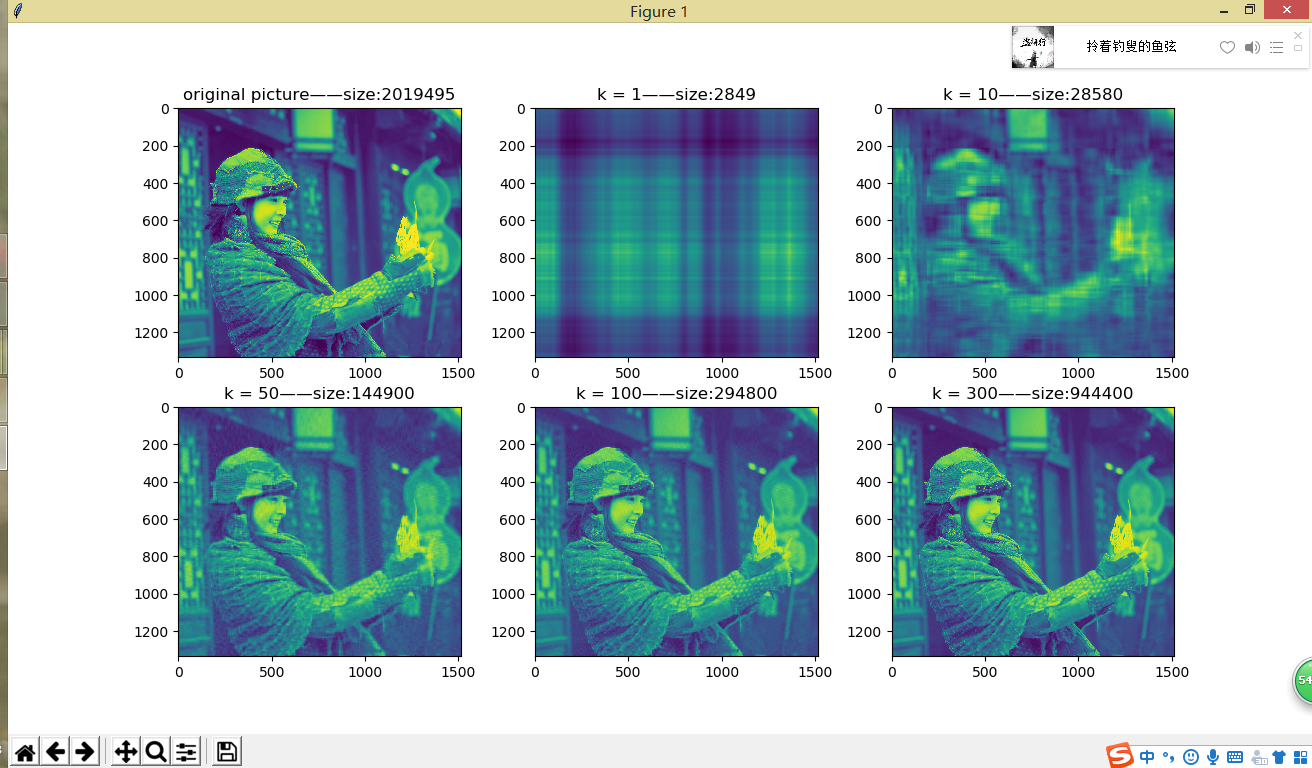
运行结果