对评分矩阵进行分解，SVD与LSI

摘自

一、SVD奇异值分解

1、SVD简介

SVD（singular value decomposition）。其作用就是将一个复杂的矩阵分解成3个小的矩阵。

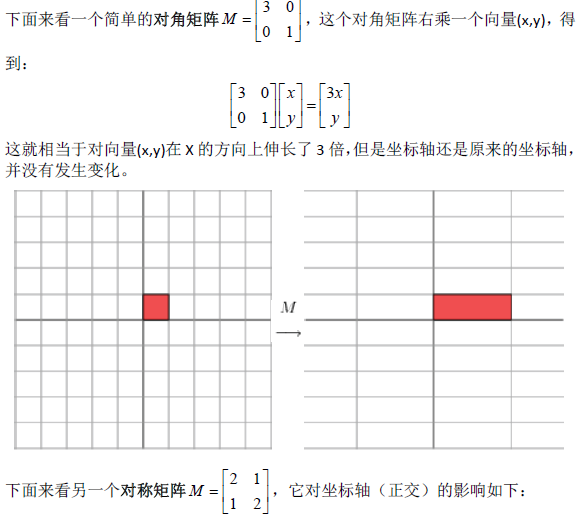
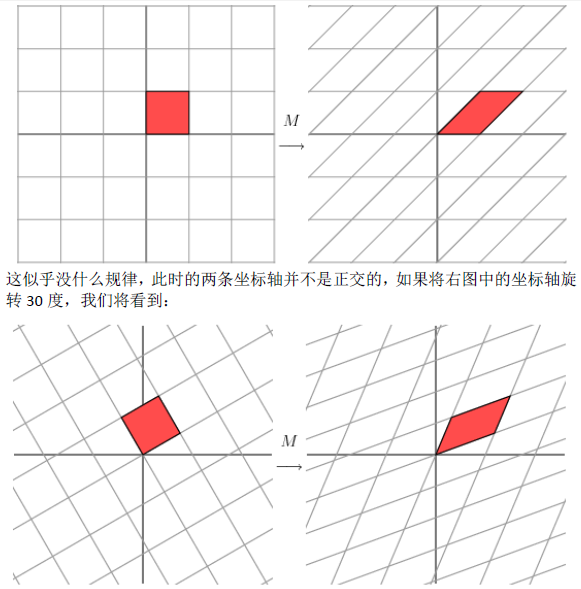
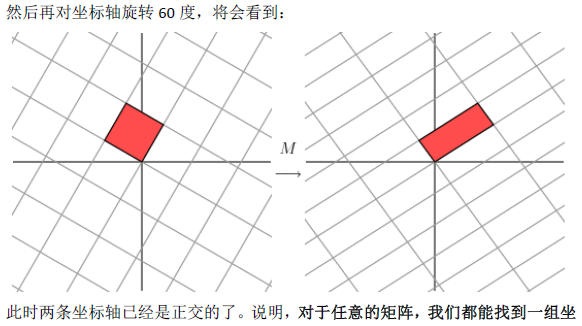
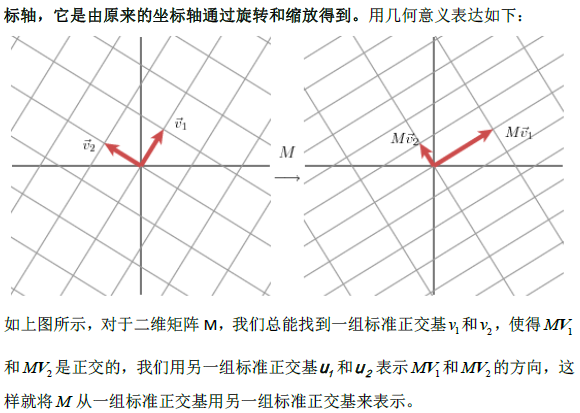
用一张图片表示SVD的结构

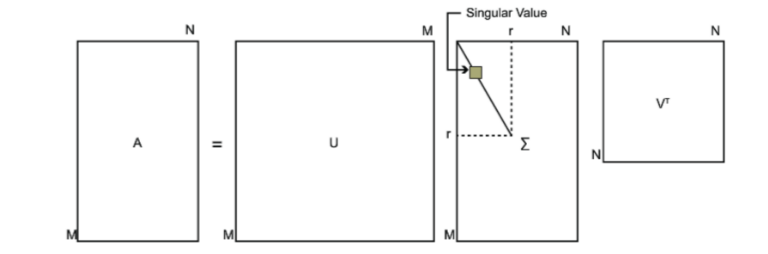
2、SVD计算

（1）特征值和特征向量

　　如果A为方阵则

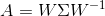
　　一般我们会把W的这nn个特征向量标准化，此时W的nn个特征向量为标准正交基

这样我们的特征分解表达式可以写成

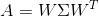
（2）当A是一般矩阵的时候

$(AA^{T})u_{i}=\lambda _{i}u_{i}$

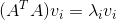
这样V和U就都求出来了。然后差奇异矩阵sigma。

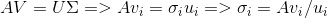
3、SVD计算例子

（1）定义矩阵A

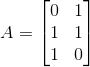
（2）

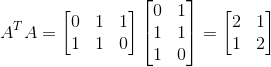
A^TA的特征值和特征向量

AA^T的特征值和特征向量

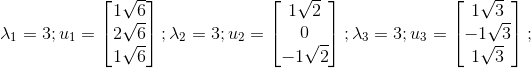
由

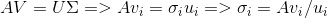可得

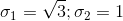
二、LSI（隐式语义索引，Latent semantic indexing）

摘自：

https://www.cnblogs.com/pinard/p/6805861.html

在文本挖掘中，主题模型是比较特殊的一块，它的思想不同于我们常用的机器学习算法，因此这里我们需要专门来总结文本主题模型的算法。本文关注于潜在语义索引算法（LSI）的原理。

1、文本主题模型的特点

　　在数据分析中，我们经常会进行非监督学习的聚类算法。它可以对我们的特征数据进行非监督的聚类。而主题模型也是非监督的算法，目的是得到文本按照主题的概率分布。从这个方面来说，主题模型和普通的聚类算法非常的类似。但是两者还是有区别的。

　　聚类算法关注样本特征。而主题模型，就是对文字中隐含主题的一种建模方法。比如从“人民的名义”和“大康书记”这两个词我们很容易发现对应的文本有很大的主题相关度。但是通过词特征来聚类的话则很难找出，因为聚类方法不能考虑到隐含的主题这一块。

　　如何找隐含的主题？常用的方法一般是基于统计学的生成方法。即假设以一定的概率选择了一个主题，然后以一定的概率选择当前主题的词。最后这些词组成了我们当前的文本。所有词的统计概率分布可以从语料库获得，具体如何以“一定的概率选择”，这就是各种具体的主题模型算法的任务了。

　　还有一些不是基于统计的算法，比如LSI

2、LSI

　　LSI有的文章也叫做LSA。LSI是基于SVD得到的文本主题的。

　　SVD公式, 有时候sigma的纬度会降低为k

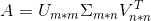
　　SVD可以这样解释：我们输入的有m个文本，每个文本有n个词。A_ij对应第i个词的第j个文本的特征值，这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数，一般要比文本数少。SVD分解后，U_il对应第i个词和第l个词义的相关度。V_jm对应第j个文本和第m个主题的相关度。Σ_lm对应第l个词和第m个主题的相关度。

　　也可以反过来解释。矩阵的各种表示方式和上面反过来。

3、LSI的举例

假设有11个词三个文本的词频TF对应矩阵如下

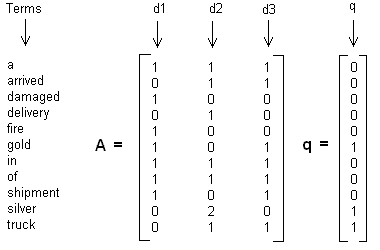
假设对应的主题数为2，则通过SVD降维后得到的三维矩阵为：

从矩阵U_k我们可以看到词和词义(个人理解就是和主题)之间的相关性。而从V可以看到3个文本和两个主题的相关性。可以看到里面有负数，这个比较难解释。

4、LSI用于文本相似度计算

LSI得到的文本主题矩阵可以用于文本相似度的计算。而计算方法一般是通过余弦相似度计算。比如对于矩阵V我们可以计算第一个文本和第二个文本的余弦相似度

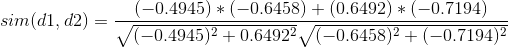
5、LSI主题模型总结

LSI可以通过一次分解就可以得到主题模型。同时解决词义的问题。但是LSI有很多不足，导致它在当前实际的主题模型中已经不再使用。

SVD计算很耗时，当词和文本数都很大时，对高纬度的矩阵进行SVD非常难。
主题值的选取对结果的影响很大，很难选择合适的k值
LSI得到的不是一个概率模型，缺乏统计基础，结果难以解释。

当需要主题模型时候，如果文本数和词很少时，使用LSI可以。其它情况可以使用LDA和HDP。