[Machine Learning] 浅谈LR算法的Cost Function

了解LR的同学们都知道，LR采用了最小化交叉熵或者最大化似然估计函数来作为Cost Function，那有个很有意思的问题来了，为什么我们不用更加简单熟悉的最小化平方误差函数（MSE）呢？

我个人理解主要有三个原因：

• MSE的假设是高斯分布，交叉熵的假设是伯努利分布，而逻辑回归采用的就是伯努利分布；
• MSE会导致代价函数$J(\theta)$非凸，这会存在很多局部最优解，而我们更想要代价函数是凸函数；
• MSE相对于交叉熵而言会加重梯度弥散。

这里着重讨论下后边两条原因。

代价函数为什么要为凸函数？

假设对于LR我们依旧采用线性回归的MSE作为代价函数：

$$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2$$

其中

$$h_{\theta}(x)=\frac{1}{1+e^{-\theta^T x}}$$

这样代价函数$J(\theta)$关于算法参数$\theta$会是非凸函数，存在多个局部解，我们可以形式化的表示为下图：

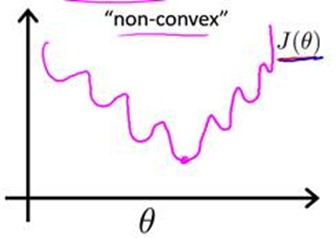
如上图所示，$J(\theta)$非常复杂，这并不是我们想要的。我们想要的代价函数是关于$\theta$的凸函数，这样我们就可以轻松地根据梯度下降法等最优化手段去轻松地找到全局最优解了。

所以，我们理想的代价函数应该是凸函数，如下图所示：

因此，MSE对于LR并不是一个理想的代价函数。那么为什么交叉熵可以呢？我们先给出交叉熵的公式形式：

$$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log{\hat{y}^{(i)}}+(1-y^{(i)})\log{(1-\hat{y}^{(i)})}]$$

即令每个样本属于其真实标记的概率越大越好，可以证明$J(\theta)$是关于$\theta$的高阶连续可导的凸函数，因此可以根据凸优化理论求的最优解。

note：最小化交叉熵也可以理解为最大化似然估计，即利用已知样本分布，找到最有可能导致这种分布的参数值，即最优解$\theta^{*}$。

为什么MSE会更易导致梯度弥散？

我们简单求解下MSE和交叉熵对应$w$的梯度，首先是MSE：

对于单样本的Loss Function为：

$$L_{MSE}=\frac{1}{2}(y-\hat{y})^{2}$$

$L_{MSE}$对于$w$的梯度为：

$$\frac{\partial L_{MSE}}{\partial w}=(y-\hat{y})\sigma(w, b)h$$

其中$\sigma(w, b)$为sigmoid函数：

$$\sigma(w, b)=\frac{1}{1+e^{-w^{T}x+b}}$$

而以交叉熵为Loss Function：

$$L_{cross\_entropy}=-(y\log{\hat{y}}+(1-y)\log(1-\hat{y}))$$

则对应的梯度为：

$$\frac{\partial L_{cross\_entropy}}{\partial w}=(\hat{y}-y)h$$

我们对比两者的梯度绝对值可以看出MSE和交叉熵两种损失函数的梯度大小差异：

$$\frac{|\Delta_{MSE}|}{|\Delta_{cross\_entropy}|}=|\sigma^{'}(w, b)| \le 0.25$$

即MSE的梯度是交叉熵梯度的1/4。

note：

• 上式为什么小于0.25可以参考另一篇博文《[Machine Learning] 深度学习中消失的梯度》
• Cost Function和Loss Function的区别
  • Cost Function：指基于参数$w$和$b$，在所有训练样本上的总成本；
  • Loss Function：指单个训练样本的损失函数。

其实可以从另外一个角度理解为什么交叉熵函数相对MSE不易导致梯度弥散：当训练结果接近真实值时会因为梯度算子极小，使得模型的收敛速度变得非常的缓慢。而由于交叉熵损失函数为对数函数，在接近上边界的时候，其仍然可以保持在高梯度状态，因此模型的收敛速度不会受损失函数的影响。