SPOJ 7001 Visible Lattice Points (莫比乌斯反演)

题意：求一个正方体里面，有多少个顶点可以在（0,0,0）位置直接看到，而不被其它点阻挡。也就是说有多少个（x,y,z）组合，满足gcd(x,y,z)==1或有一个0，另外的两个未知数gcd为1

定义f(t)为gcd(x,y,z)==t或有一个0，另外的两个未知数gcd为t的组合数

定义F（x）为 ∑p(t)   x|t  =  （n/x）* (n/x) * (n/x+3)

那么满足下面的

则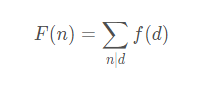

求出f(1)即为答案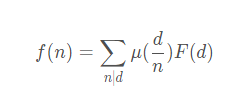

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=1000000+10;
ll is[maxn],pri[maxn],u[maxn],cnt;
void getu()
{
    u[1]=1;
    for(int i=2;i<maxn;i++)
    {
        if(is[i]==0)
        {
            cnt++;
            pri[cnt]=i;
            u[i]=-1;
        }
        for(int j=1;j<=cnt;j++)
        {
            ll k=pri[j]*i;
            if(k>=maxn)break;
            is[k]=1;
            if(i%pri[j]==0)u[k]=0;
            else u[k]=-u[i];
        }
    }
}
int main()
{
    getu();
//    for(int i=1;i<=100;i++)
//        cout<<i<<" "<<u[i]<<endl;
    int T;
    scanf("%d",&T);
    while(T--)
    {
        ll n;
        scanf("%lld",&n);
        ll num=3;
        for(int i=1;i<=n;i++)
            num+=u[i]*(n/i)*(n/i)*(n/i+3);
        printf("%lld\n",num);
    }
    return 0;
}