HDU 1542"Atlantis"（线段树+扫描线求矩形面积并）

传送门

•题意

　　给你 n 矩形，每个矩形给出你 $(x_1,y_1),(x_2,y_2)$ 分别表示这个矩形的左下角和右上角坐标；

　　让你求这 n 个矩形并的面积；

　　其中 $x \leq 10^{5} \ ,\ y \leq 10^{5}$;

•题解

　　这类题的解决方法需要用到一个比较重要的算法--扫描线算法；

　　其实并不需要将扫描线算法学的多么透彻，此类题仅仅用到了扫描线算法的思想；

　　下面开始说说如何用扫描线处理这类问题；

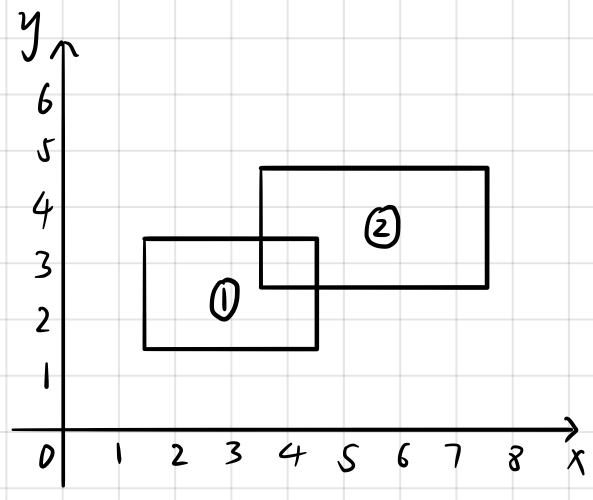
　　假设你有两个矩形，如图所示；

　　　　

　　矩形①的左下角和右上角坐标分别为：$(1.2\ ,\ 1.4),(4.5\ ,\ 3.4)$

　　矩形②的左下角和右上角坐标分别为：$(3.5\ ,\ 2.6),(7.6\ ,\ 4.8)$

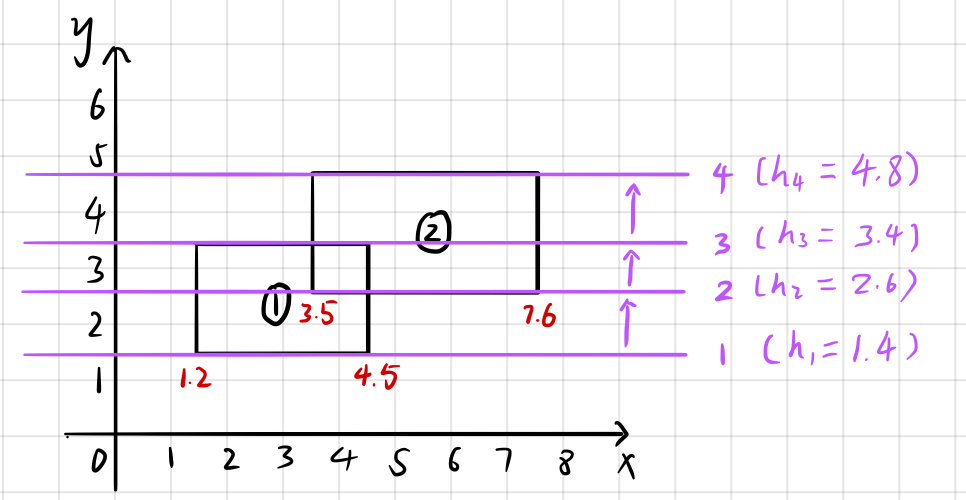
　　现在，假想有一条扫描线，从上到下扫描整个多边形；

　　　　

　　扫描线从1位置开始扫描，计算出扫描线1扫描到的矩形的长度 $line_{1}=4.5-1.2 = 3.3$；

　　扫描线从1位置向上扫描，来到2位置，计算出扫描线1,2扫描到的矩形面积 $area_{1}=line_{1} \times (h_2-h_1)$；

　　并计算出扫描线2扫描到的矩形的长度 $line_{2}=7.6-1.2=6.4$；

　　扫描线从2位置向上扫描，来到3位置，计算出扫描线2,3扫描到的矩形面积 $area_{2}=line_{2} \times (h_{3}-h_{2})$；

　　并计算出扫描线3扫描到的矩形的长度 $line_{3}=7.6-3.5=4.1$；

　　扫描线从3位置向上扫描，来到4位置，计算出扫描线3,4扫描到的矩形面积 $area_{3}=line_{3} \times (h_{4}-h_{3})$；

　　到这，就通过扫描线求出了矩形并的面积 $area=area_{1}+area_{2}+area_{3}$；

　　通过上述模拟，便可知道，要想用扫描线，那么，你需要做好如下准备工作：

　　　　（1）保存好矩形的上下边

　　　　（2）按照高度将保存的信息排序

　　那么，该如何记录呢？

　　我们可以用结构体来保存所有的上下边，结构定义如下：

 struct Data
 {
     double l,r;///保存边的左右信息
     double h;///保存边的高度
     int f;///判断该边为所在矩形的上边还是下边，上边就赋值为-1，下边赋值为1
     bool operator < (const Data &obj)const///按照边的高度升序排列
     {
         return h < obj.h;
     }
 }a[maxn<<];

　　那么，将上述两个矩形的边存入 a 中并排好序后的信息为：

　　　　$a_{1}:\{l=1.2\ ,\ r=4.5\ ,\ h=1.4\ ,\ f=1 \}$

　　　　$a_{2}:\{l=3.5\ ,\ r=7.6\ ,\ h=2.6\ ,\ f=1 \}$

　　　　$a_{3}:\{l=1.2\ ,\ r=4.5\ ,\ h=3.4\ ,\ f=-1 \}$

　　　　$a_{4}:\{l=3.5\ ,\ r=7.6\ ,\ h=4.8\ ,\ f=-1 \}$

　　因为坐标较大，所以需要将横坐标离散化；

•Code

　　HDU1542.cpp