初学maven的一些配置

初学Maven的一些配置

1.maven的安装

2.从官网下载3.6.1版本后，高级版本可能会出现不兼容 jdk1.8

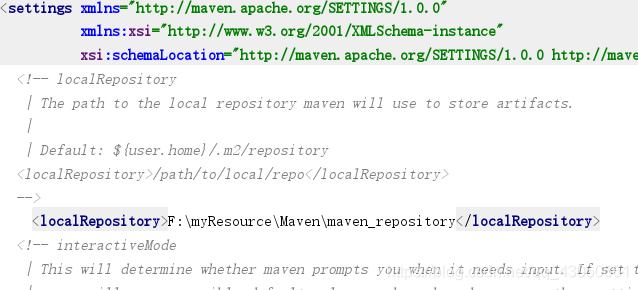
3.配置maven 在 settings.xml <settings>标签中

4. 在你安装maven的目录 我的--》F:\myResource\Maven\apache-maven-3.6.1\conf

/path/to/local/repo
-->

<localRepository>F:\myResource\Maven\maven_repository</localRepository>

将maven本地存储库改为其他盘存放，下载的jar包都将导入到此文件夹下

安装目录不要有中文路径

5.配置 <miroor>

<!-- nexus-aliyun 首选，放第一位,有不能下载的包，再去做其他镜像的选择  -->

<!--    <mirror>-->
<!--      <id>alimaven</id>-->
<!--      <mirrorOf>central</mirrorOf>-->
<!--      <name>aliyun maven</name>-->
<!--      <url>https://maven.aliyun.com/repository/central</url>-->
<!--    </mirror>-->

<!-- 备选镜像，也是可以通过 url 去查找确定一下，
    该镜像是否含有你想要的包，速度较慢，但类库全  -->

<!--    <mirror>-->
<!--      <id>central-repository</id>-->
<!--      <mirrorOf>central</mirrorOf>-->
<!--      <name>Central Repository</name>-->
<!--      <url>https://repo1.maven.org/maven2/</url>-->
<!--    </mirror>-->

maven远程仓库在国外，下载速度较慢，可选用国内的镜像仓库，多个仓库只执行第一个

在 F:\myResource\Maven\apache-maven-3.6.1\conf\ settings.xml 配置

如果还出现报错，则注释 mirror配置部分，

则配置

<!--这个是阿里私服仓库 ， 使用mirror  添加一直报错，也可选这个-->

<profiles>
	<profile>
     <repositories>
       <repository>
         <name>aliyunmaven</name>
         <id>aliyunmaven</id>
         <url>http://maven.aliyun.com/nexus/content/groups/public/</url>
       </repository>
     </repositories>
   </profile>
</profiles>

<!--或者  <url>https://maven.aliyun.com/repository/central</url> -->

6.idea 配置maven

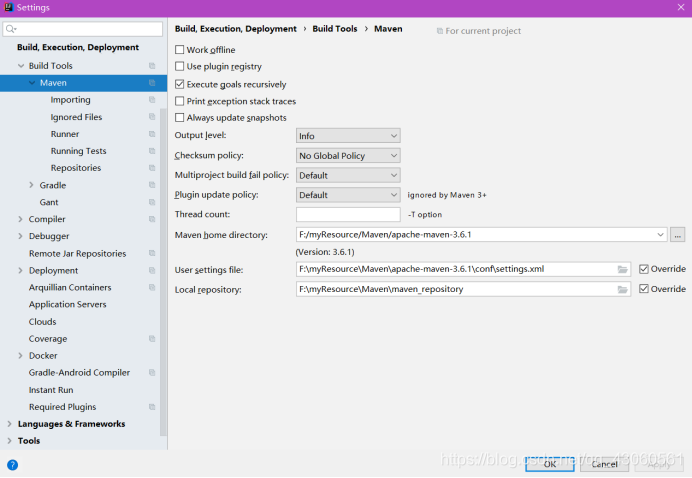
maven home directory:  maven安装的目录
User settings file: maven安装的目录\conf\settings.xml
Local repository:   用户本地maven仓库存放位置

7.配置 Runner

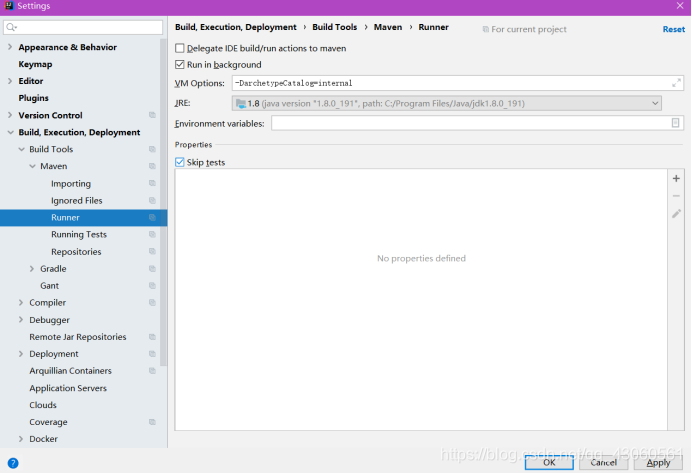
-DarchetypeCatalog=internal   -->>可以判断本地仓库是否有所需jar包，有则不下载，否则反之

在
F:\myResource\Maven\maven_repository\org\apache\maven\archetype\archetype-catalog\3.0.1
目录下添加   archetype-catalog.xml文件（百度下载）

创建idea 提供的 maven构建模板，



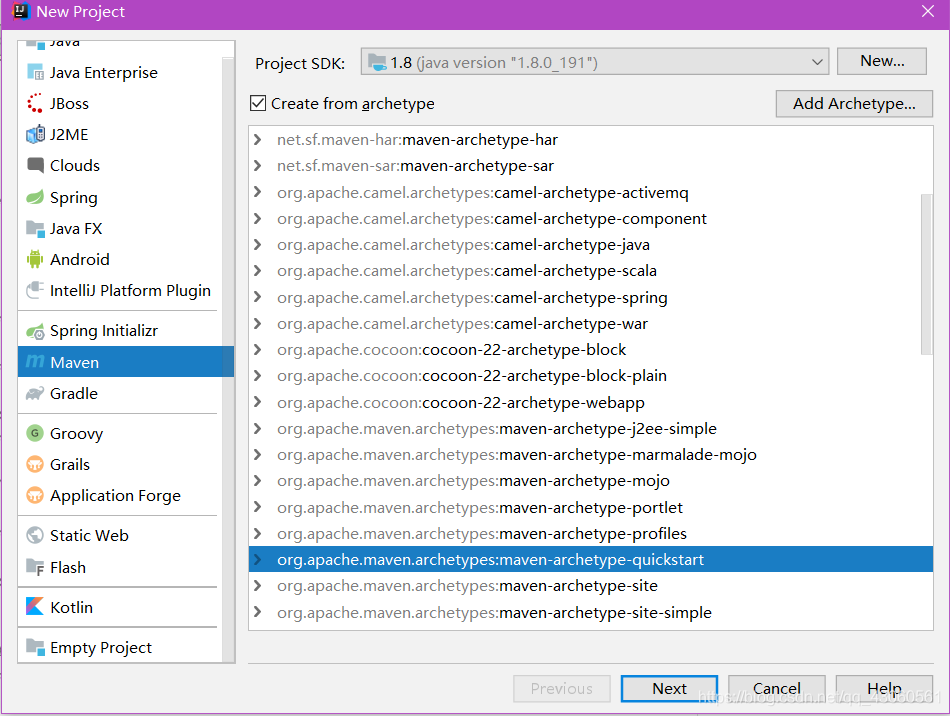
选apache.maven.archetypes:maven-archetype,

不要wicket,会出现很多奇怪错误

over，不足之处请指正