APP上传应用商店加固后打包

在cmd进入jdk的bin目录，把keystore文件和apk安装包放到bin目录下，然后执行以下命令，需要管理员权限：

jarsgner -verbose -sigalg SHA1withRSA -digestalg SHA1 -keystore [keystorePath] -singnedjar [apkOut] [apkln] [alias]

例如

jarsigner -verbose -sigalg SHA1withRSA -digestalg SHA1 -keystore androids.keystore -signedjar mzbl36000.apk mzbl3600.apk 00000000000

jarsgner -verbose -sigalg SHA1withRSA -digestalg SHA1 -keystore [keystorePath] -singnedjar [apkOut] [apkln] [alias]

ps：红色英文不填的话，默认签名算法采用“SHA256withRSA”，所以会导致360提示：”您的应用签名算法采用“SHA256withRSA”，在部分4.2一下安卓版本的手机上不能安装

详细

Android版本加固后签名 
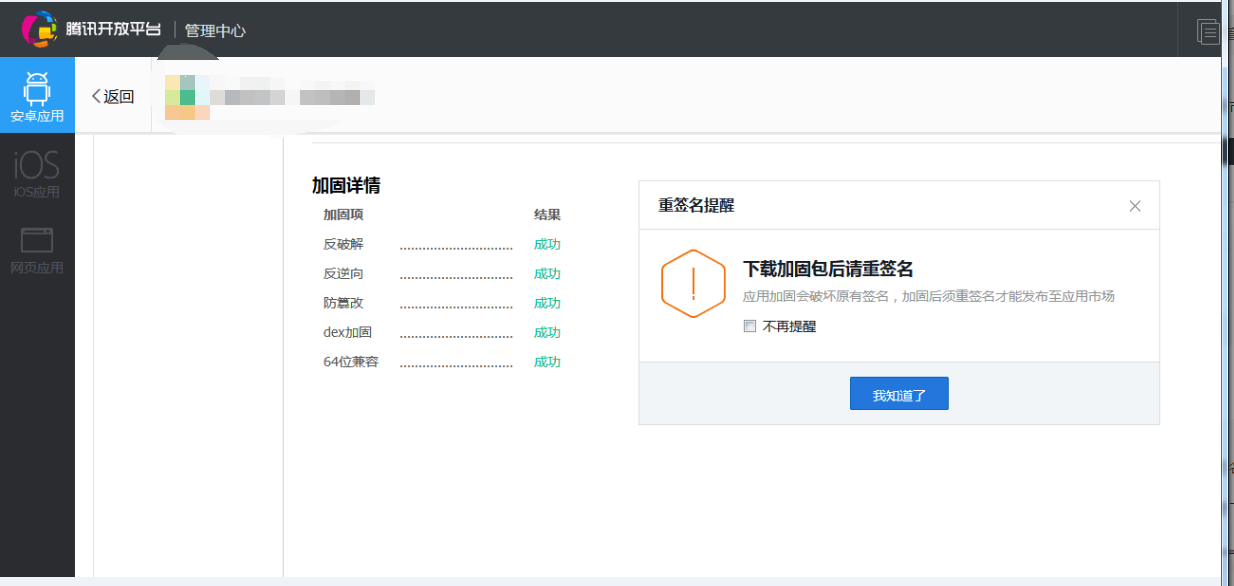
在上传应用的时候，应用加固之后会破坏原有的签名，需要重新签名才能发布到应用市场中，如下图： 

加固后的签名步骤如下： 
1：签名之前需要Java的JDK环境以及被破坏签名的apk安装包，以及将需要用来签名的keystore文件。 
2：将未签名的apk和keystore文件拷贝到JDK安装目录下bin子目录下，通过bin目录下的jarsigner命令对未签名的apk安装包进行签名。 
通过cmd进入命令行模式： 
1、 Windows+R 
 
2、 输入如下命令进行签名： 
jarsigner -verbose –keystore 指定数字证书存储路径 
-signedjar 签名后的apk包未签名的 apk包_legu.apk 数字证书别名 
如： 
jarsigner -verbose -keystore mzjsz.keystore -signedjar zjsz_android_release-release.apk zjsz_android_release-release.apk zjsz 
以上命令的说明： 
-verbose：指定生成详细输出 
-keystore：指定数字证书存储路径 
-signedjar：该选项的三个参数为 
签名后的apk包 
未签名的apk包 
数字证书别名（后面有获取方式） 
注意数字证书别名有效期。 
注意：签名后的apk包和未签名的apk包的包名尽量不要相同，否则将会将之前的版本直接覆盖掉。 
输入正确指令之后会要求输入密钥库的密码即keystore的File Password，输入的过程中不会有任何的显示。输入完成按Enter键： 
 
接着输入密钥口令即keystore的Key Password，完成按Enter 
 
当出现下图即表示成功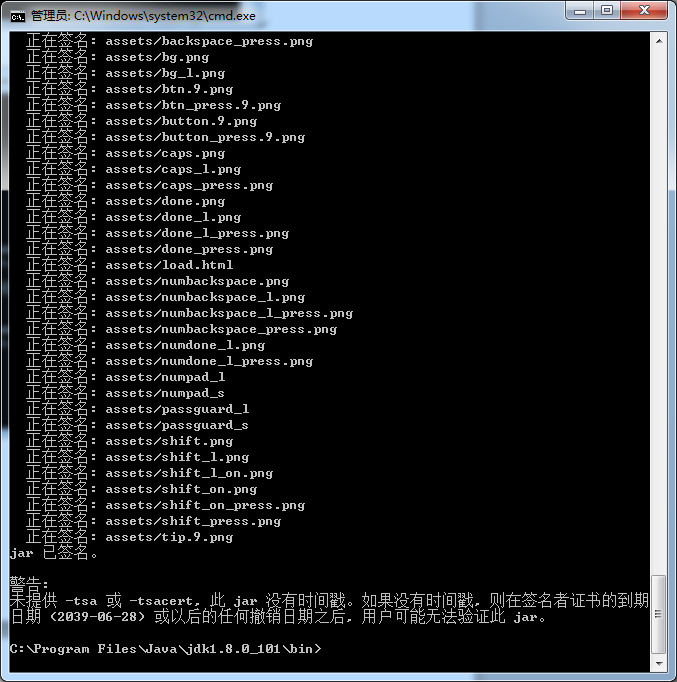 
 
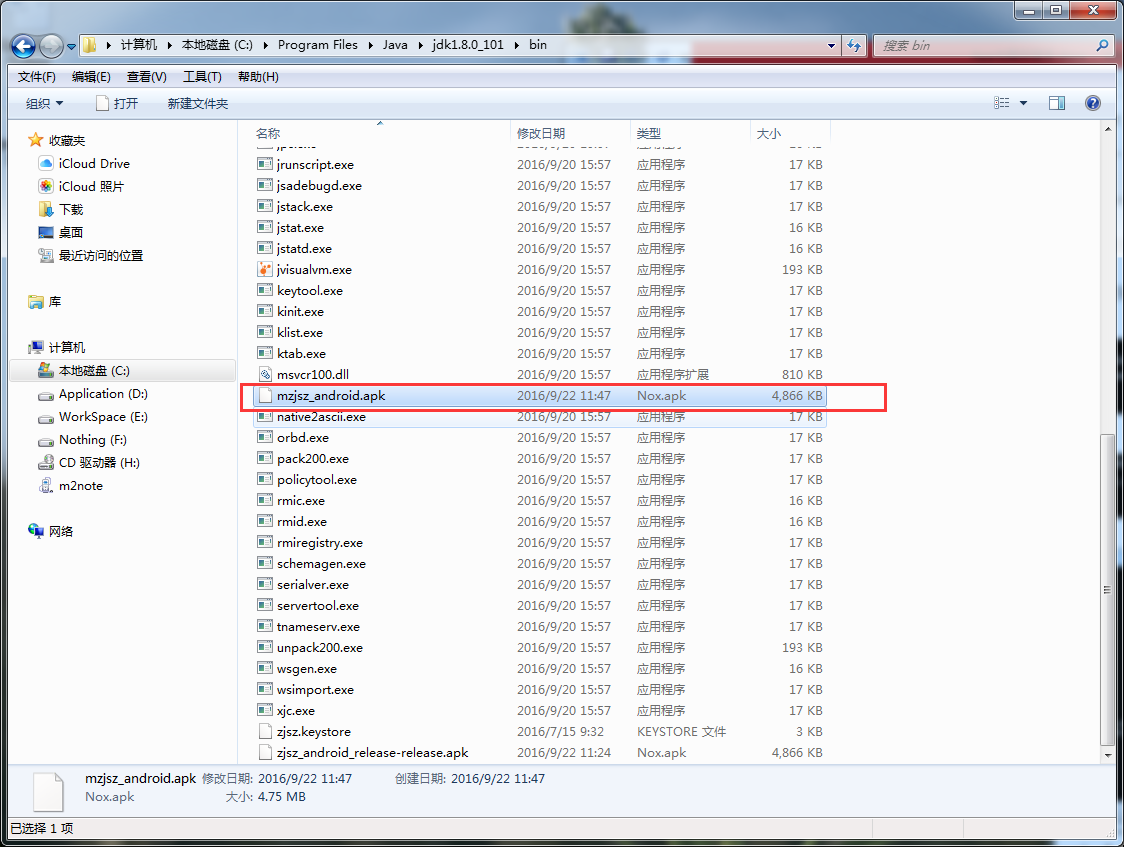
在bin目录下生成一个mzjsz_android.apk文件。 

获取keystore数字证书别名： 
在签名的过程中会需要获取keystore数字证书别名，具体的操作如下： 
通过命令定位在JDK的bin目录下，或者在bin文件夹中按住shift+右键，在弹出菜单项中选择在此处打开命令窗口。 
输入指令keytool -list -v -keystore keystore文件名 –storepass keystore文件密码 
例如：keytool -list -v -keystore keystoreName -storepass keystorePassword 
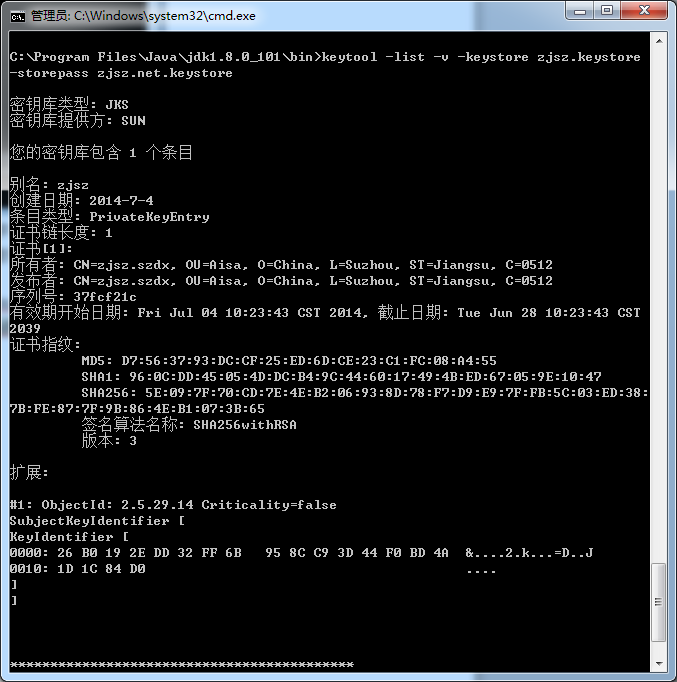
出现下图就表示获取成功