【数据结构】【平衡树】浅析树堆Treap

【Treap】

【Treap浅析】

　　Treap作为二叉排序树处理算法之一，首先得清楚二叉排序树是什么。对于一棵树的任意一节点，若该节点的左子树的所有节点的关键字都小于该节点的关键字，且该节点的右子树的所有节点的关键字都大于该节点的关键字，则这棵树是一棵二叉排序树。

　　Treap在每一个节点中有两个最关键的元素——weight和value。

　　value是在创建这个新节点时赋予该节点的数值大小，Treap利用每个节点的value值将整棵树维持成一个二叉排序树。

　　weight是在创建这个新节点时赋予该节点的伪随机数，Treap利用每个节点的weight值将整棵树维持成一个最小堆（或最大堆）。

　　看似不相容的二叉排序树和堆的结合却正是Treap的关键之处。如果用递增（或递减）数列只是对单纯的二叉排序树进行插入操作的话可以想见会变成这种情况：

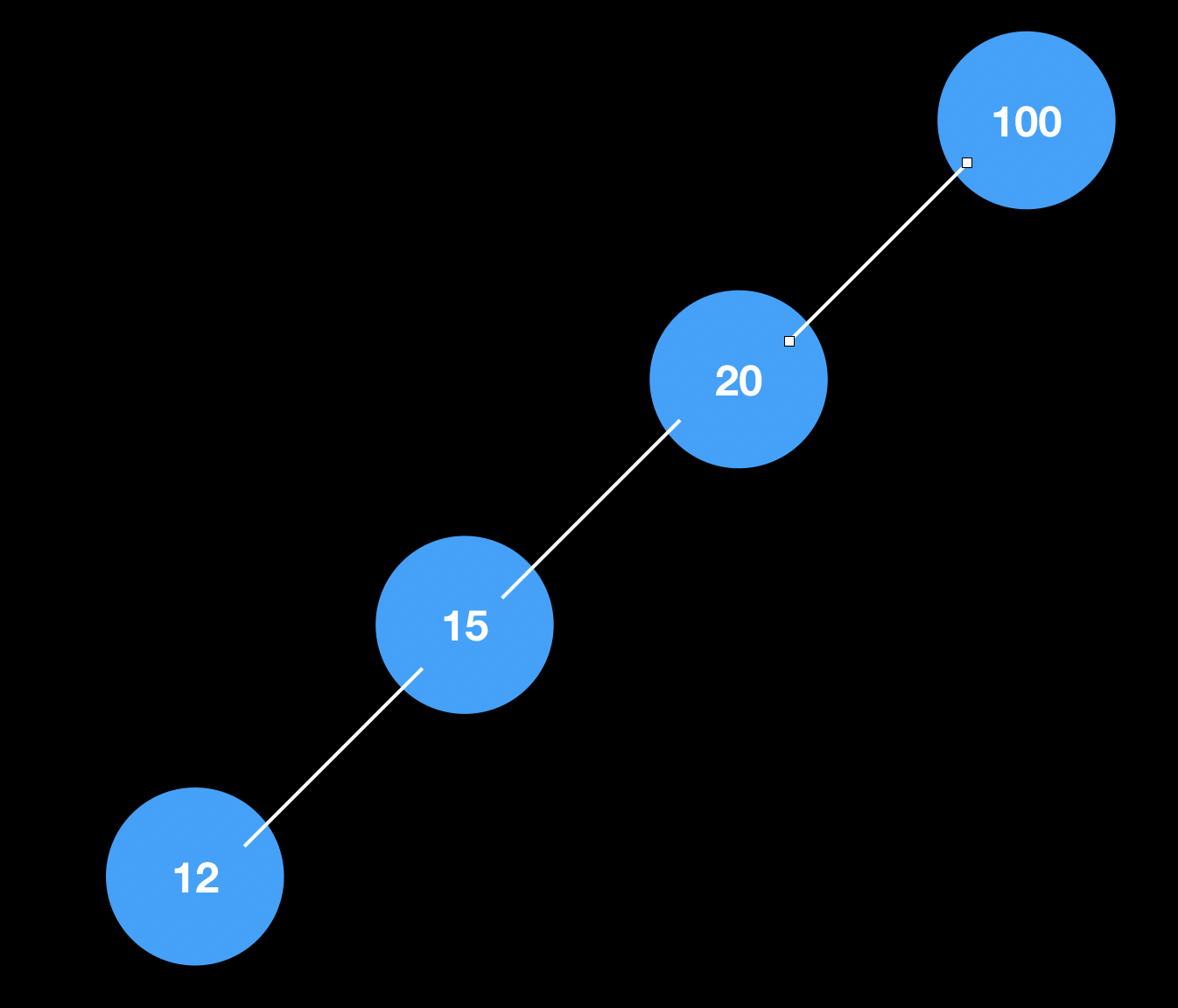
　　此时一棵二叉搜索树就退化成了数链，每次对树上进行查询都会退化成O（N）。而利用随机数的随机性把二叉树维护成一个堆，就可以尽量使一条不严格数链维护成一棵伪平衡树。

　　那Treap是如何同时维护堆和二叉搜索树的呢？这就涉及到旋转操作。

　　Treap涉及两种旋转操作：左旋和右旋。这里用最小堆举例子（懒得用电脑画图（逃：

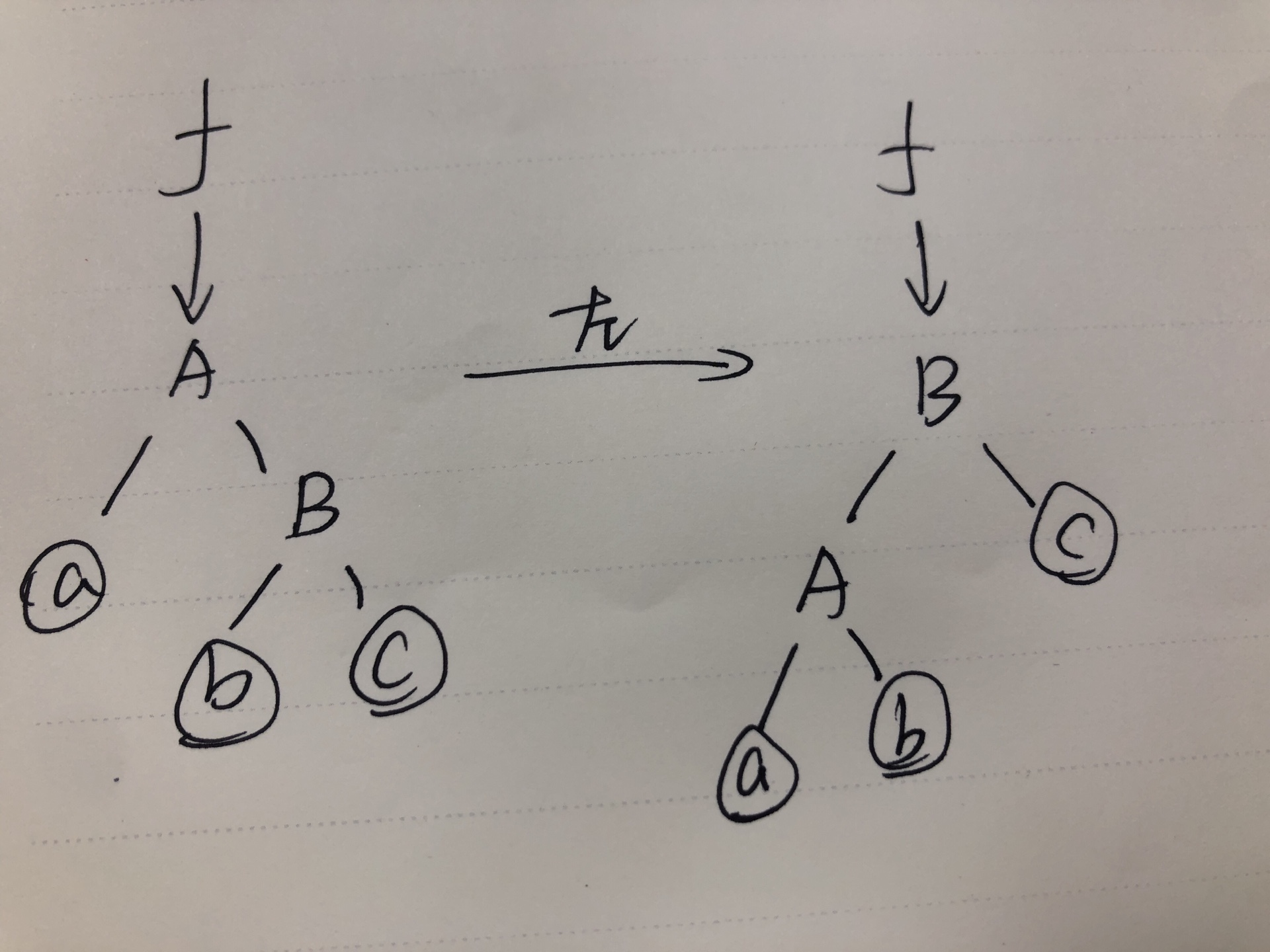
　　利用代码看一下左、右旋代码的实现：

　　1.左旋：

 void lt(int &k){
     int tmp = t[k].r;
     t[k].r = t[tmp].l;
     t[tmp].l = k;
     t[tmp].size = t[k].size;
     t[k].size = t[t[k].l].size + t[t[k].r].size + t[k].cnt;
     k = tmp;
 }

　　2.右旋：

 void rt(int &k){
     int tmp = t[k].l;
     t[k].l = t[tmp].r;
     t[tmp].r = k;
     t[tmp].size = t[k].size;
     t[k].size = t[t[k].r].size + t[t[k].l].size + t[k].cnt;
     k = tmp;
 }

　　除了旋转之外还有许多其他的操作，结合代码看一下：

　　插入节点：

 void Insert(int &k,int num){
     if(!k){//如果这是一个没有被创建过的新的节点就创建一个新的节点
         k = ++size;
         t[k].wt = rand();//为该新节点赋予一个随机值weight
         t[k].val = num;//为该节点赋予一个数值大小value
         t[k].cnt = t[k].size = ;
         return ;
     }
     ++t[k].size;//插入了一个新节点，所以路径上每个结点的子树大小++
     if(num == t[k].val){//如果这个数值被添加到树中过，就把那个节点处的cnt++
         ++t[k].cnt;
         return ;
     }
     if(num < t[k].val){//如果要被插入的数值比当前结点数值小，向左子树寻找
         Insert(t[k].l,num);
         if(t[t[k].l].wt < t[k].wt)//如果左右孩子其中一个不满足最小堆，即其中一个小于父亲节点，则通过旋转使其满足最小堆
             rt(k);
     }
     else{//如果要被插入的数值比当前结点数值大，向右子树寻找
         Insert(t[k].r,num);
         if(t[t[k].r].wt < t[k].wt)//维护最小堆
             lt(k);
23 }

　　删除节点：

  void Delete(int &k,int num){
      if(!k)
          return ;
      if(t[k].val == num){
          if(t[k].cnt > ){//如果某个数值被插入2次及以上，在节点处cnt--即可。
              --t[k].cnt;
              --t[k].size;
              return ;
          }
          else if(!(t[k].l * t[k].r)){//如果那个数值只被插入了一次且左右孩子至少有一个为空，则直接把不为空的孩子接到父亲节点上。
              k = t[k].l + t[k].r;
              return ;
          }
          else{//如果两个孩子都不为空，则把两个孩子中weight较小的旋转到父亲节点，把原来的要删除的节点一直旋转成叶子节点或只有一个非空孩子的节点。
              if(t[t[k].l].wt <= t[t[k].r].wt){
                  rt(k);
                  Delete(k,num);
              }
              else{
                  lt(k);
                  Delete(k,num);
              }
          }
      }
      else{
          --t[k].size;//经过的路径size全都--
          if(num < t[k].val)//判断接下来寻找num位置的走向
              Delete(t[k].l,num);
          else
              Delete(t[k].r,num);
      }
 }

　　求序列中某一数值在数列中的排名：

 int Rank(int &k,int num){
     if(!k)
         return ;
     if(t[k].val == num)
         return t[t[k].l].size + ;//若与当前结点相等，左节点size+1就是排名，防止t[k].cnt影响排名
     else if(t[k].val > num)
         return Rank(t[k].l,num);
     else
         return Rank(t[k].r,num) + t[t[k].l].size + t[k].cnt;//递归到右子树返回的是在右子树之内的排名，要加上父节点的cnt和左孩子的size
 }

　　求序列中第k大数值：

 int Search(int &k,int num){
     if(!k)
         return ;
     if(num <= t[t[k].l].size)
         return Search(t[k].l,num);
     else if(num <= t[t[k].l].size + t[k].cnt)//如果排名属于(左孩子size，左孩子size + 当前结点cnt]区间内，则第k大数就是该节点的数值大小。
         return t[k].val;
     else
         return Search(t[k].r,num - t[t[k].l].size - t[k].cnt);//进行右子树的递归，排名需剪掉左子树的size和当前结点cnt，这样才能保证在右子树找到正确结果。
 }

　　求前序及后序：

 int Pre(int &k,int num){
     if(!k)
         return -2147483648;//返回极小值避免对下方max函数产生影响
     if(t[k].val >= num)
         return Pre(t[k].l,num);
     else
         return max(t[k].val,Pre(t[k].r,num));//如果当前结点数值小于num，则在该节点右子树寻找比该节点数值更大的节点，后序同理
 }
 int Nex(int &k,int num){
     if(!k)
         return 2147483647;
     if(t[k].val <= num)
         return Nex(t[k].r,num);
     else
         return min(t[k].val,Nex(t[k].l,num));
 }

　　这就是比其他平衡树要好写的多的Treap了。Treap功能十分局限，但有个Treap2.0叫作无旋Treap，功能就和其他平衡树相差无几了，学了再更。