【BZOJ1272】Gate Of Babylon [Lucas][组合数][逆元]

Gate Of Babylon

Time Limit: 10 Sec  Memory Limit: 162 MB
[Submit][Status][Discuss]

Description

　　

Input

　　

Output

　　

Sample Input

　　2 1 10 13

　　3

Sample Output

　　12
　　

HINT

　　

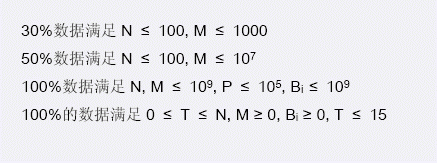
Main idea

　　有若干个没有限制的道具，以及T个有限制个数的道具，取出m个，求方案数。

Solution

　　首先，看到有限制的只有15个，因此可以考虑使用容斥原理：Ans=全部没有限制的方案-有1个超过限制的方案数+有2个超过限制的方案数-有3个超过限制的方案数…。

　　以此类推。我们先考虑没有限制的，在m组无限制的数中选n个的方案数，显然就是C(n+m-1,n)。

　　因为这道题是要求不超过m的方案数，也就是那么运用加法原理，发现答案也就是C(n+0-1,0)+C(n+1-1,1)+C(n+2-1,2)+...+C(n+m-1,m)=C(n+m,m)。

　　然后考虑有限制的情况，有一个超过限制直接用总数减去（这个的限制+1)就是当前的总数，相当于强制要选限制+1个为空。

　　然后只要DFS，记录到当前为止选了几个，答案要记是b[i]+1,判断加减，最后累加答案。

　　最后，n、m过大，发现p是一个质数，所以可以用Lucas定理：Lucas(n,m,p)=Lucas(n/p,m/p,p)*C(n%p,m%p)，其中C(n%p,m%p)求的时候要用到乘法逆元。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;  

 const int ONE=;

 int n,T,m,MOD;
 long long Ans;
 long long Jc[ONE];
 int b[ONE];

 int get()
 {
         int res,Q=;    char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 long long Quickpow(int a,int b,int MOD)
 {
         long long res=;
         while(b)
         {
             if(b&) res=res*a%MOD;
             a=(long long)a*a%MOD;
             b/=;
         }
         return res;
 }

 int C(int m,int n)
 {
         if(m<n) return ;
         int up=Jc[m]%MOD;
         int down=(long long)Jc[m-n]*Jc[n]%MOD;
         return (long long)up*Quickpow(down,MOD-,MOD)%MOD;
 }

 int Lucas(int n,int m,int MOD)
 {
         long long res=;
         if(n<m) return ;
         while(n && m)
         {
             res=res*C(n%MOD,m%MOD)%MOD;
             n/=MOD; m/=MOD;
         }
         return res;
 }

 void Dfs(int len,int PD,int val)
 {
         if(len==T+)
         {
             Ans+=PD*Lucas(n+m-val,m-val,MOD);
             Ans+=MOD;
             Ans%=MOD;
             return;
         }
         Dfs(len+,PD,val);
         Dfs(len+,-PD,val+b[len]+);
 }

 int main()
 {
         n=get();    T=get();    m=get();    MOD=get();
         Jc[]=; for(int i=;i<=MOD;i++) Jc[i]=(long long)Jc[i-]*i%MOD;
         for(int i=;i<=T;i++)
         b[i]=get();
         Dfs(,,);
         printf("%d",Ans);
 }