洛谷P1605走迷宫

传送

这是一道dfs,但是...但是....但是它竟然被放在bfs练习题辣！！！！

打了半天bfs，发现路径不会标记了，于是发现好像有什么不对的，似乎dfs要简单一点，于是半路跑去打dfs,结果打了半天没有输出。。。。又跑回来打bfs。。。。如此循环n遍，甚至找了bfs的题解，但是...蒟蒻到看不懂。回去深思dfs,突然发现没有把走过的路径标记下来......崩溃.....悲伤......&%&^$&^&*^*%&^%(&*^*&%&&^^&((^*&(&*^&^&%&^#$%$$^&%^#$^&(*&^(*^&^&&*(&*()

（某人崩溃到乱码ing）

好了刚才我什么都没有说。

为什么说这道题不是bfs而是dfs呢？

首先，题目要求的是走到终点的方案数，而不是最小步数

如果是求最小步数，那当然是用bfs了。但这里求的是方案数，也就是走到一次终点，ans++,然后把这条路径重新标记为没走过。（回溯）用bfs,也就是把每一步的坐标加入队列。为什么说他不方便回溯呢？这和bfs的搜索顺序有关

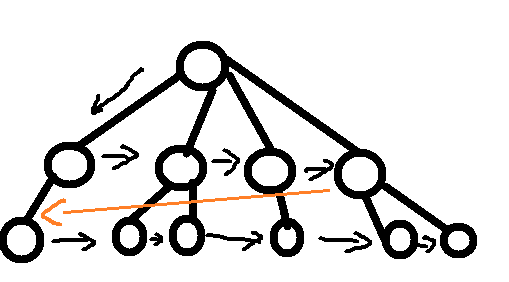
箭头为bfs每个节点出现的顺序，所以当我们用bfs走到出口时，会发现该节点的父亲节点的位置已经跑到十万八千里之外了，并且还不能由出队得到父亲节点。

当然，这里有位大神用bfs做的。bfs题解（这是所有的题解...）

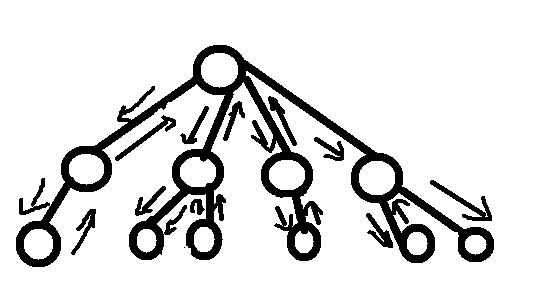
这是dfs每个节点出现的顺序,这样回溯到父亲节点就简单多了，直接回溯一步就行，所以这个题选用dfs解法（也就是套个模板）

在此复习一下dfs的模板（from c++一本通）

模板一：

int dfs(k)
{
   for(int i=;i<=maxn;i++)//maxn是变化方式的总数
    {if(操作合法)
         {保存结果；
           if(到达目的地)
              {输出解；return ;
               }
            dfs(k+);
             回溯;
          }
     }
}

模板二：

void dfs(k)
{
    if(到达目标){输出解; return;}
    for(int i=;i<=maxn;i++)
    {  if(操作合法)
          {标记;
              dfs(k+);
             回溯;
           }
     }
}

好了我们开始套模板

#include<iostream>
#include<cstdio>
using namespace std;
int k,n,m,t,sx,sy,fx,fy,dx[]={,-,,},dy[]={,,,-},ans,ljx[],ljy[];
int zx[],zy[];
bool vis[][],bl[][];
bool hf(int x,int y)
{ if(x<||x>n||y<||y>m)return ;
   for(int i=;i<=t;i++)
   if(x==zx[i]&&y==zy[i])return ;
   if(vis[x][y])return ;
   return ;
}
void search(int x,int y)
{
   if(x==fx&&y==fy)//一个模板
     {ans+=;vis[x][y]=;return ;
     }
   for(int i=;i<=;i++)//四个方向
   { int xx=x+dx[i],yy=y+dy[i];//从当前的x,y向四个方向走（走到下一步时的x与y就是这一步的xx和yy,所以不必有x+=dx[i],y+=dy[i]
     if(hf(xx,yy))
     { vis[xx][yy]=;//在判断中以是否走过为主要依据 （原因：每个格只走一次）
      search(xx,yy);
      vis[xx][yy]=;//回溯
     }
   }
}
int main()
{   scanf("%d%d%d",&n,&m,&t);
    scanf("%d%d%d%d",&sx,&sy,&fx,&fy);
    for(int i=;i<=t;i++)
    {scanf("%d%d",&zx[i],&zy[i]);
      vis[zx[i]][zy[i]]=;//标记走过
    }
    vis[sx][sy]=;
     search(sx,sy);
     printf("%d",ans);
}

qwq