NOI2012 : 迷失游乐园

终于补完NOI2012了好开心~

题目大意：给定一棵树或者环套外向树，求出从中随机选一条简单路径的期望长度，环上点数不超过20。

设

d[x]表示x的度数，ch[x]表示x孩子个数

up[x]表示x向上走的期望长度，down[x]表示x向下走的期望长度

f[x]表示x的父亲

树的情况：

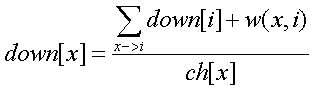
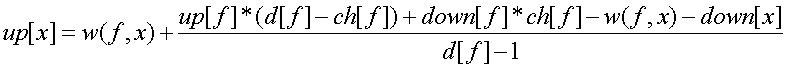
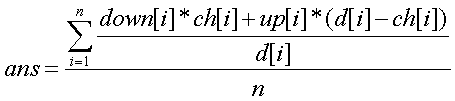
环套外向树的情况：

先找出环，对于每棵树用之前的方法求出down[]

对环上每个点i顺时针逆时针各走一圈，求出up[i]：

up[i]=sum((i走到j的概率)*(way(i,j)+down[j])*(j往它孩子走的概率))

i走到j的概率分两种情况讨论，

以顺时针为例，

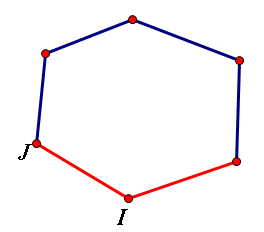
第一步由于要确定是顺时针还是逆时针，所以顺时针走概率为0.5，

之后每一步概率/=(上一个点孩子数+1)

j往它孩子走的概率分两种情况讨论，

以顺时针为例，

每一步向下走概率为该点孩子数/(该点孩子数+1)，最后一步由于不可能回到i点，所以向下走概率为1

然后用树的方法求出其它点的up[]

再统计ans即可

没加任何优化居然跑了Rank1…

#include<cstdio>
#define N 100010
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
int n,m,i,j,x,y,z;
int g[N],nxt[N<<1],w[N<<1],v[N<<1],ed,pre[N],ch[N],d[N],fw[N],st,sum;
int cnt,a[N<<1],s[N<<1];
double up[N],down[N],ans,p;
bool vis[N],in[N];
inline void add(int x,int y,int z){d[x]++;v[++ed]=y;w[ed]=z;nxt[ed]=g[x];g[x]=ed;}
void dfs1(int x,int f){
  for(int i=g[x];i;i=nxt[i])if(v[i]!=f&&!in[v[i]])dfs1(v[i],x),ch[x]++,down[x]+=down[v[i]]+w[i];
  if(ch[x])down[x]/=ch[x];
}
void dfs2(int x,int f){
  for(int i=g[x];i;i=nxt[i])if(v[i]!=f&&!in[v[i]]){
    up[v[i]]=w[i];
    if(d[x]>1)up[v[i]]+=(up[x]*(d[x]-ch[x])+down[x]*ch[x]-w[i]-down[v[i]])/(d[x]-1);
    dfs2(v[i],x);
  }
}
void find(int x,int f,int l){
  if(st)return;
  pre[x]=f;fw[x]=l;
  if(vis[x]){st=f;return;}
  vis[x]=1;
  for(int i=g[x];i;i=nxt[i])if(v[i]!=f)find(v[i],x,w[i]);
}
int main(){
  for(read(n),read(m);i<m;i++)read(x),read(y),read(z),add(x,y,z),add(y,x,z);
  if(m<n)dfs1(1,0),dfs2(1,0);else{
    find(1,0,0);
    for(in[a[cnt=1]=st]=1,i=pre[st];i!=st;i=pre[i])in[a[++cnt]=i]=1;
    for(i=1;i<=cnt;i++)a[i+cnt]=a[i],s[i+1]=s[i+cnt+1]=fw[a[i]];
    for(i=1;i<=cnt;i++)dfs1(a[i],0);
    for(i=1;i<=cnt;i++){
      //i->j
      j=i+1;p=0.5;sum=s[j];
      up[a[i]]+=p*(sum+down[a[j]])*ch[a[j]]/(ch[a[j]]+1);
      p/=ch[a[j]]+1;
      for(j=i+2;j<i+cnt-1;j++){
        sum+=s[j];
        up[a[i]]+=p*(sum+down[a[j]])*ch[a[j]]/(ch[a[j]]+1);
        p/=ch[a[j]]+1;
      }
      j=i+cnt-1;
      sum+=s[j];
      up[a[i]]+=p*(sum+down[a[j]]);
      //j<-i
      j=i+cnt-1;p=0.5;sum=s[j+1];
      up[a[i]]+=p*(sum+down[a[j]])*ch[a[j]]/(ch[a[j]]+1);
      p/=ch[a[j]]+1;
      for(j=i+cnt-2;j>i+1;j--){
        sum+=s[j+1];
        up[a[i]]+=p*(sum+down[a[j]])*ch[a[j]]/(ch[a[j]]+1);
        p/=ch[a[j]]+1;
      }
      j=i+1;
      sum+=s[j+1];
      up[a[i]]+=p*(sum+down[a[j]]);
    }
    for(i=1;i<=cnt;i++)dfs2(a[i],0);
  }
  for(i=1;i<=n;i++)ans+=(down[i]*ch[i]+up[i]*(d[i]-ch[i]))/d[i];
  printf("%.5f",ans/n);
  return 0;
}