地精部落：dp

Description

传说很久以前，大地上居住着一种神秘的生物：地精。 地精喜欢住在连绵不绝的山脉中。具体地说，一座长度为 N 的山脉 H可分 为从左到右的 N 段，每段有一个独一无二的高度 Hi，其中Hi是1到N 之间的正 整数。 如果一段山脉比所有与它相邻的山脉都高，则这段山脉是一个山峰。位于边 缘的山脉只有一段相邻的山脉，其他都有两段（即左边和右边）。 类似地，如果一段山脉比所有它相邻的山脉都低，则这段山脉是一个山谷。 地精们有一个共同的爱好——饮酒，酒馆可以设立在山谷之中。地精的酒馆 不论白天黑夜总是人声鼎沸，地精美酒的香味可以飘到方圆数里的地方。 地精还是一种非常警觉的生物，他们在每座山峰上都可以设立瞭望台，并轮 流担当瞭望工作，以确保在第一时间得知外敌的入侵。 地精们希望这N 段山脉每段都可以修建瞭望台或酒馆的其中之一，只有满足 这个条件的整座山脉才可能有地精居住。 现在你希望知道，长度为N 的可能有地精居住的山脉有多少种。两座山脉A 和B不同当且仅当存在一个 i，使得 Ai≠Bi。由于这个数目可能很大，你只对它 除以P的余数感兴趣。

Input

仅含一行，两个正整数 N, P。

Output

仅含一行，一个非负整数，表示你所求的答案对P取余 之后的结果。

Sample Input

4 7

Sample Output

3

Hint

对于 20%的数据，满足 N≤10；
对于 40%的数据，满足 N≤18；
对于 70%的数据，满足 N≤550；
对于 100%的数据，满足 3≤N≤4200，P≤10910^910​9​​

101810^{18}10​18​​,1<=q<=10510^510​5​​

为什么这是组合数呢？

有两种方法，都是n²，一种需要组合数，另一种不需要。

我因为算错数了，推式子的时候排除了这两种方法。。。最后才捡回来

Solution 1

设dp[i][j][st]表示目前你构成的山长度为i，以相对高度为j的山结尾，末端下降和上扬的状态分别以st的0，1表示。

想不出怎么递推？打表啊！

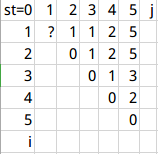
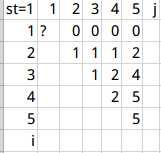
dp[1][1][]太特殊会被算2遍，不考虑。

发现两个表貌似只是上下倒置了，打出一个就可以。以st=1的表为例。

找规律（嘤嘤嘤我找了3天呢）：dp[i][j]=∑_k=1->jdp[i-1][i-k]

式子的含义是什么呢？假如我们想要长度为i，最后一座山在这i个高度的高度排名为第j。

我们把最后一座山拿走，那么如果倒数第二座山的高度比最后一座高，那么它的排名-1。否则不变。

因为趋势需要上扬，dp[i][j][0]+=dp[i-1][k][1];k<j

再考虑到倒置的问题就得到了那个式子。

 #include<cstdio>
 int mod,n,dp[][],ans;
 inline int modd(int p){return p>=mod?p-mod:p;}
 int main(){
     dp[][]=;
     scanf("%d%d",&n,&mod);
     for(int i=;i<=n;++i)for(int j=;j<=i;++j)dp[i&][j]=modd(dp[i&][j-]+dp[i&^][i-j+]);
     for(int j=;j<=n;++j)ans=modd(ans+dp[n&][j]);
     printf("%d",modd(ans<<));
 }

317字节

Solution 2考虑假如你已经造出了两座山，现在需要合并它们。

考虑到所有情况，将不同的数分给两座山的情况用组合数计算。

这是可实现的，和排列计数类似，但是我没有实现，就不多说了。

公式什么的看代码吧。

 #include<cstdio>
 int C[][],dp[][];
 int main(){
     int n,p,now=;
     scanf("%d%d",&n,&p);
     dp[][]=dp[][]=C[][]=C[][]=dp[][]=dp[][]=;
     for(int i=;i<=n;i++,now^=){
         C[now][]=;C[now][i]=;
         for(int j=;j<i;j++){
             if(j) C[now][j]=(C[now^][j]+C[now^][j-])%p;
             dp[i][(i-j-)%]=(dp[i][(i-j-)%]+1ll*dp[j][]*dp[i-j-][(i-j-)%]%p*C[now^][j]%p)%p;
         }
     }
     printf("%d",(dp[n][]+dp[n][])%p);
 }

来自奶牛mikufun