最短路径(Floyd算法）

声明：图片及内容基于https://www.bilibili.com/video/BV1oa4y1e7Qt?from=articleDetail

多源最短路径的引入

Floyd算法

原理

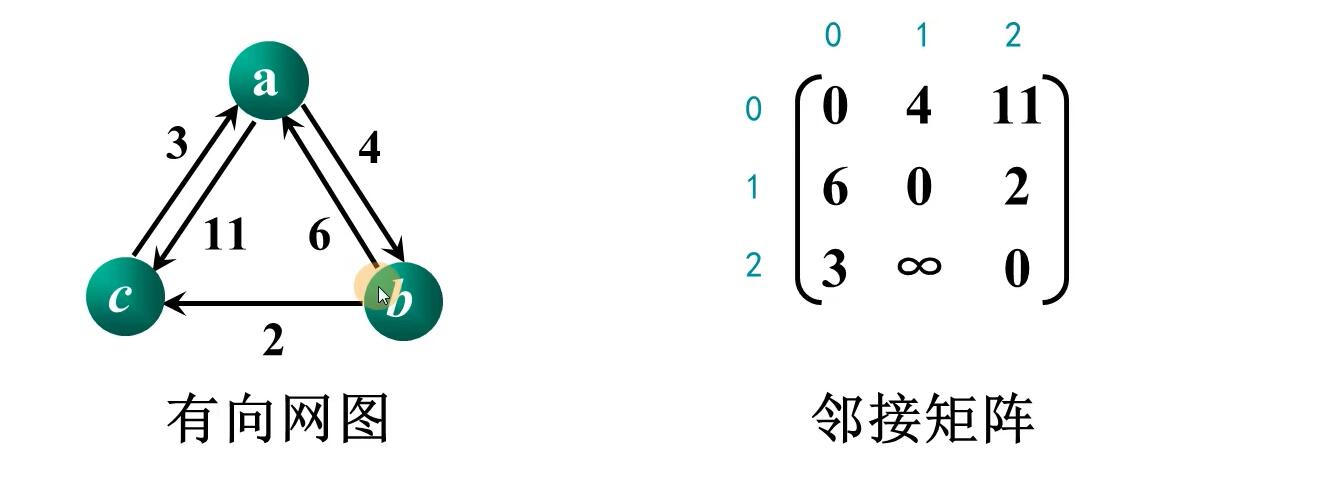
加入a：

加入b：

加入c：

数据结构

核心代码

Floyd()

void MGraph::Floyd(){
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            dist[i][j]=arc[i][j];                    //dist数组初始化
            if(dist[i][j]!=INFINIT&&dist[i][j]!=0) //dist为INFINIT则无路径，dist为0则指向自己
                path[i][j]=vertex[i]+vertex[j];    //path数组初始化
            else
                path[i][j]="";                     //不符合则path为空串
        }
    }
    for(int k=0;k<vertexNum;k++){                  //k个顶点循环k次
        for(int i=0;i<vertexNum;i++){              //k每循环一次，要更新dist和path数组
            for(int j=0;j<vertexNum;j++){
                if(dist[i][k]+dist[k][j]<dist[i][j]){
                    dist[i][j]=dist[i][k]+dist[k][j];
                    //这里两个path拼接的时候，第一个字符串的最后一个字符和第二个字符串的第一个字符重复
                    //用substr去除第一个字符串的最后一个字符
                    string tmp=path[i][k].substr(0,path[i][k].length()-1);
                    path[i][j]=tmp+path[k][j];
                }
            }
        }
    }
    displayDist();
    displayPath();
}

完整代码

#include<iostream>
#define MAX 50
#define INFINIT 65535
#include <string>
using namespace std;
class MGraph{
    private:
        int vertexNum,arcNum;    //顶点数，边数
        int arc[MAX][MAX];       //邻接矩阵
        string vertex[MAX];  //顶点信息
        int dist[MAX][MAX];
        string path[MAX][MAX];
    public:
        MGraph(string v[],int n,int e);
        void display();
        void Floyd();
        void displayDist();
        void displayPath();
};
void MGraph::Floyd(){
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            dist[i][j]=arc[i][j];                    //dist数组初始化
            if(dist[i][j]!=INFINIT&&dist[i][j]!=0) //dist为INFINIT则无路径，dist为0则指向自己
                path[i][j]=vertex[i]+vertex[j];    //path数组初始化
            else
                path[i][j]="";                     //不符合则path为空串
        }
    }
    for(int k=0;k<vertexNum;k++){                  //k个顶点循环k次
        for(int i=0;i<vertexNum;i++){              //k每循环一次，要更新dist和path数组
            for(int j=0;j<vertexNum;j++){
                if(dist[i][k]+dist[k][j]<dist[i][j]){
                    dist[i][j]=dist[i][k]+dist[k][j];
                    //这里两个path拼接的时候，第一个字符串的最后一个字符和第二个字符串的第一个字符重复
                    //用substr去除第一个字符串的最后一个字符
                    string tmp=path[i][k].substr(0,path[i][k].length()-1);
                    path[i][j]=tmp+path[k][j];
                }
            }
        }
    }
    displayDist();
    displayPath();
}
void MGraph::displayDist(){             //打印dist数组
    cout<<"dist数组："<<endl;
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            cout<<dist[i][j]<<"\t";
        }
        cout<<endl;
    }
}
void MGraph::displayPath(){             //打印path数组
    cout<<"path数组：" <<endl;
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            cout<<path[i][j]<<"\t";
        }
        cout<<endl;
    }
}
MGraph::MGraph(string v[],int n,int e){   //n是顶点数，e是边数
    vertexNum=n;
    arcNum=e;
    for(int i=0;i<vertexNum;i++){
        vertex[i]=v[i];
    }
    for(int i=0;i<arcNum;i++){        //初始化邻接矩阵
        for(int j=0;j<arcNum;j++){
            if(i==j) arc[i][j]=0;
            else arc[i][j]=INFINIT;
        }
    }
    int vi,vj,w;
    for(int i=0;i<arcNum;i++){
        cout<<"请输入有向边的两个顶点和这条边的权值"<<endl;
        cin>>vi>>vj>>w;   //输入边依附的两个顶点的编号 和权值
        arc[vi][vj]=w; //有边标志
    }
}
void MGraph::display(){
    cout<<"邻接矩阵："<<endl;
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            if(arc[i][j]==INFINIT)
                cout<<"∞"<<"\t";
            else cout<<arc[i][j]<<"\t";
        }
        cout<<endl;
    }
    cout<<endl;
    cout<<"结点信息："<<endl;
    for(int i=0;i<vertexNum;i++){
        cout<<vertex[i]<<" ";
    }
    cout<<endl;
}
int main(){
    int n,e;
    string v[MAX];
    cout<<"请输入顶点数和边数"<<endl;
    cin>>n>>e;
    cout<<"请输入顶点信息"<<endl;
    for(int i=0;i<n;i++){
        cin>>v[i];
    }
    MGraph mgraph(v,n,e);
    mgraph.display();
    mgraph.Floyd();
    return 0;
}

输入：

3 5
a b c
0 1 4
0 2 11
1 0 6
1 2 2
2 0 3

输出：

邻接矩阵：
0 4 11
6 0 2
3 ∞ 0

结点信息：
a b c
dist数组：
0 4 6
5 0 2
3 7 0
path数组：
　　 ab   abc
bca 　     bc
ca   cab

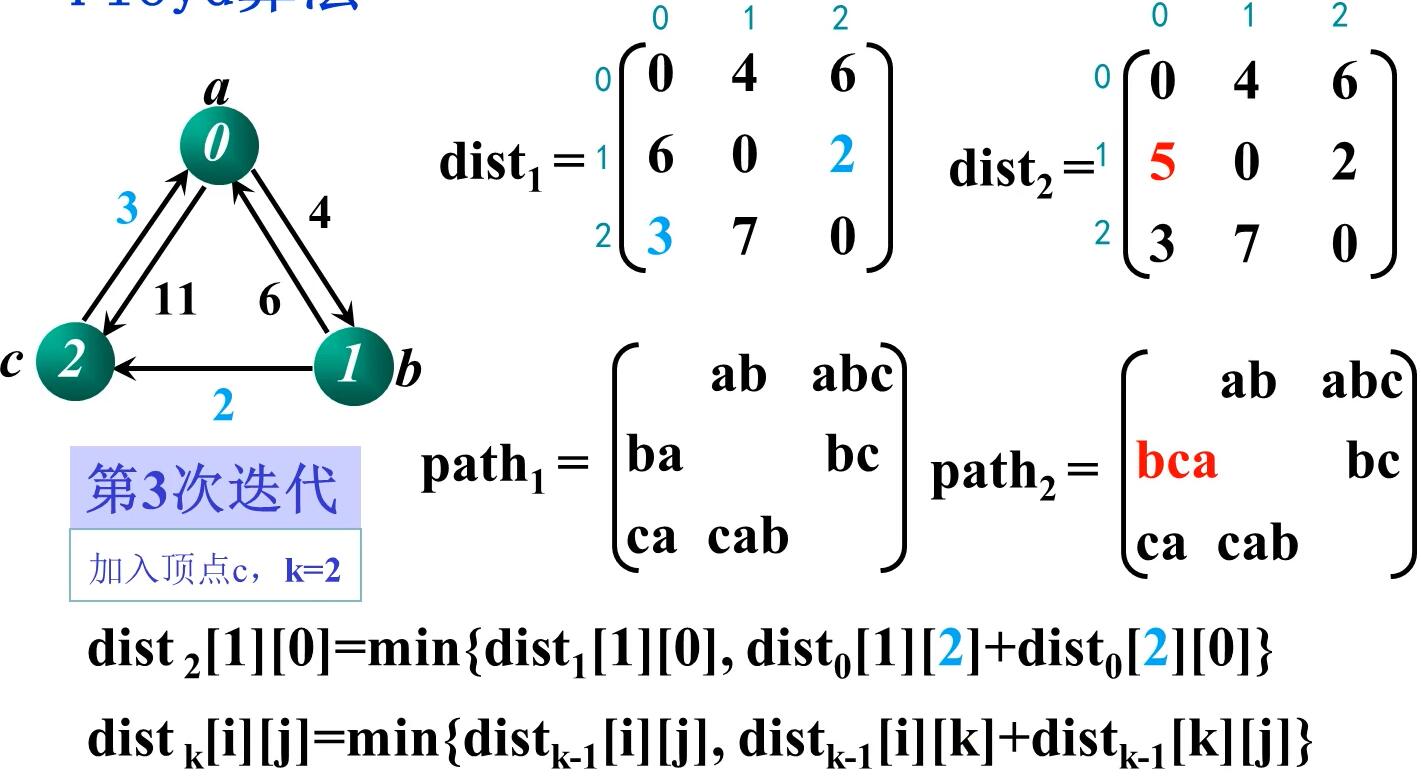
例题：娱乐中心选址

#include<iostream>
#define MAX 50
#define INFINIT 65535
#include <string>
using namespace std;
class MGraph{
    private:
        int vertexNum,arcNum;    //顶点数，边数
        int arc[MAX][MAX];       //邻接矩阵
        string vertex[MAX];  //顶点信息
        int dist[MAX][MAX];
        string path[MAX][MAX];
        int rowSum[MAX];
        int rowMax[MAX];
    public:
        MGraph(string v[],int n,int e);
        void display();
        void Floyd();
        void displayDist();
        void displayPath();
        void bestCentralAmusement();
        void displayRowMax();
        void displayRowSum();
};
void MGraph::bestCentralAmusement(){
    for(int i=0;i<vertexNum;i++)
        rowSum[i]=0;
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            rowSum[i]+=dist[i][j];
        }
    }
    int tmp;
    for(int i=0;i<vertexNum;i++){
        tmp=0;
        for(int j=0;j<vertexNum;j++){
            if(tmp<dist[i][j]) tmp=dist[i][j];
        }
        rowMax[i]=tmp;
    }
    int tmp2=INFINIT;
    int index=-1;
    for(int i=0;i<vertexNum;i++){
        if(rowMax[i]<tmp2){
            tmp2=rowMax[i];
            index=i;
        }
        if(tmp2==rowMax[i]){
            if(rowSum[i]<tmp2){
                index=i;
            }else{
                ;
            }
        }
    }
    displayRowMax();
    displayRowSum();
    cout<<"index:"<<index<<endl;
    cout<<"最合适的位置是"<<vertex[index]<<endl;
}
void MGraph::displayRowSum(){
    cout<<"rowSum: "<<endl;
    for(int i=0;i<vertexNum;i++)
        cout<<rowSum[i]<<" ";
    cout<<endl;
}
void MGraph::displayRowMax(){
    cout<<"rowMax:"<<endl;
    for(int j=0;j<vertexNum;j++)
        cout<<rowMax[j]<<" ";
    cout<<endl;
}
void MGraph::Floyd(){
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            dist[i][j]=arc[i][j];                    //dist数组初始化
            if(dist[i][j]!=INFINIT&&dist[i][j]!=0) //dist为INFINIT则无路径，dist为0则指向自己
                path[i][j]=vertex[i]+vertex[j];    //path数组初始化
            else
                path[i][j]="";                     //不符合则path为空串
        }
    }
    for(int k=0;k<vertexNum;k++){                  //k个顶点循环k次
        for(int i=0;i<vertexNum;i++){              //k每循环一次，要更新dist和path数组
            for(int j=0;j<vertexNum;j++){
                if(dist[i][k]+dist[k][j]<dist[i][j]){
                    dist[i][j]=dist[i][k]+dist[k][j];
                    //这里两个path拼接的时候，第一个字符串的最后一个字符和第二个字符串的第一个字符重复
                    //用substr去除第一个字符串的最后一个字符
                    string tmp=path[i][k].substr(0,path[i][k].length()-1);
                    path[i][j]=tmp+path[k][j];
                }
            }
        }
    }
    displayDist();
    displayPath();
}
void MGraph::displayDist(){             //打印dist数组
    cout<<"dist数组："<<endl;
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            cout<<dist[i][j]<<"\t";
        }
        cout<<endl;
    }
}
void MGraph::displayPath(){             //打印path数组
    cout<<"path数组：" <<endl;
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            cout<<path[i][j]<<"\t";
        }
        cout<<endl;
    }
}
MGraph::MGraph(string v[],int n,int e){   //n是顶点数，e是边数
    vertexNum=n;
    arcNum=e;
    for(int i=0;i<vertexNum;i++){
        vertex[i]=v[i];
    }
    for(int i=0;i<arcNum;i++){        //初始化邻接矩阵
        for(int j=0;j<arcNum;j++){
            if(i==j) arc[i][j]=0;
            else arc[i][j]=INFINIT;
        }
    }
    int vi,vj,w;
    for(int i=0;i<arcNum;i++){
        cout<<"请输入有向边的两个顶点和这条边的权值"<<endl;
        cin>>vi>>vj>>w;   //输入边依附的两个顶点的编号 和权值
        arc[vi][vj]=w; //有边标志
    }
}
void MGraph::display(){
    cout<<"邻接矩阵："<<endl;
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            if(arc[i][j]==INFINIT)
                cout<<"∞"<<"\t";
            else cout<<arc[i][j]<<"\t";
        }
        cout<<endl;
    }
    cout<<endl;
    cout<<"结点信息："<<endl;
    for(int i=0;i<vertexNum;i++){
        cout<<vertex[i]<<" ";
    }
    cout<<endl;
}
int main(){
    int n,e;
    string v[MAX];
    cout<<"请输入顶点数和边数"<<endl;
    cin>>n>>e;
    cout<<"请输入顶点信息"<<endl;
    for(int i=0;i<n;i++){
        cin>>v[i];
    }
    MGraph mgraph(v,n,e);
    mgraph.display();
    mgraph.Floyd();
    mgraph.bestCentralAmusement();
    return 0;
}

输入：

5 10
a b c d e
0 1 13
0 3 4
1 0 13
1 2 15
1 4 5
2 3 12
3 0 4
3 2 12
4 2 6
4 3 3

输出：

邻接矩阵：
0   13 ∞  4  ∞
13  0 15 ∞  5
∞  ∞  0  12 ∞
4  ∞  12  0  ∞
∞  ∞  6   3  0

结点信息：
a b c d e
dist数组：
0  13  16  4 18
12  0  11  8  5
16 29  0 12 34
4  17  12 0  22
7  20   6  3  0
path数组：
ab adc ad abe
beda bec bed be
cda cdab cd cdabe
da dab dc dabe
eda edab ec ed
rowMax:
18 12 34 22 20
rowSum:
51 36 91 55 36
index:1
最合适的位置是b