统计学三大相关性系数：pearson，spearman，kendall

在文献以及各种报告中，我们可以看到描述数据之间的相关性：pearson correlation，spearman correlation，kendall correlation。它们分别是什么呢？计算公式？怎样用R语言简单实现计算呢？本文一一介绍~
建议前期阅读：协方差与相关系数-“傻傻”也能分清

总的来讲，三个相关性系数（pearson, spearman, kendall）反应的都是两个变量之间变化趋势的方向以及程度，其值范围为-1到+1，0表示两个变量不相关，正值表示正相关，负值表示负相关，值越大表示相关性越强

person correlation coefficient（皮尔森相关性系数-r）

公式：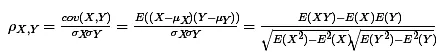

两个变量(X, Y)的皮尔森相关性系数(ρX,Y)等于它们之间的协方差cov(X,Y)除以它们各自标准差的乘积(σX, σY)。（分母是变量的标准差，这就意味着变量的标准差不能为0（分母不能为0），也就是说你每个变量所包含值不能都是相同的。如果没有变化，方差为0，那么是无法计算的）

方差是表示一个变量的波动情况，方差越小表示数据越集中，越大表示数据越离散；
标准差：等于（或近似等于）方差的开根号；
协方差：可以理解成两个变量之间的方差，其取值可以是负无穷到正无穷，它可以表示两个变量之间的变化趋势，但是不能表示它们之间的程度

局限性：

实验数据通常假设是成对的来自于正态分布的总体。为啥通常会假设为正态分布呢？因为我们在求皮尔森相关性系数以后，通常还会用t检验之类的方法来进行皮尔森相关性系数检验。
实验数据之间的差距不能太大，或者说皮尔森相关性系数受异常值的影响比较大。因为根据公式可以看到是直接是用x，y的值进行计算。相对应的spearman correlation对异常值不敏感，因为它是属于rank test，具体见下面介绍。

spearman correlation coefficient（斯皮尔曼相关性系数-p）

通常也叫斯皮尔曼秩相关系数。

“秩”，可以理解成就是一种顺序或者排序，那么它就是根据原始数据的排序位置进行求解，而不是直接是用x，y的值进行求解（因此对异常值不敏感，也不要求正态分布）。
公式：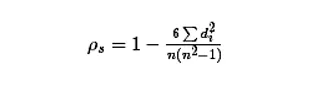

计算过程就是：

获得秩次：记下原始X Y值得排序位置（X’, Y’），（X’, Y’）的值就称为秩次
对两个变量（X, Y）的数据进行排序
计算两个变量秩次的差值，也就是上面公式中的di，n就是变量中数据的个数
最后带入公式就可求解结果。
举个例子吧，假设我们实验的数据如下：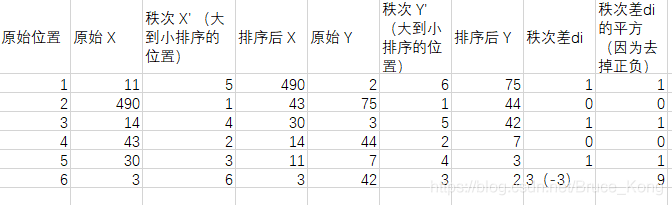

带入公式，求得斯皮尔曼相关性系数：ρ(s)= 1-6*(1+1+1+9)/6*35=0.657
不用管X和Y这两个变量具体的值到底差了多少，只需要算一下它们每个值所处的排列位置的差值，就可以求出相关性系数了。（如果原始数据中有重复值，则在求秩次时要以它们的平均值为准）

优势：

即便在变量值没有变化的情况下，也不会出现像皮尔森系数那样分母为0而无法计算的情况。
即使出现异常值，由于异常值的秩次通常不会有明显的变化（比如过大或者过小，那要么排第一，要么排最后），所以对斯皮尔曼相关性系数的影响也非常小
斯皮尔曼相关性系数没有那些数据条件要求，适用的范围广

pearson和spearman都是衡量连续型变量间的相关性，那么如果是分类变量呢？

kendall correlation coefficient（肯德尔相关性系数-k）

肯德尔相关性系数，又称肯德尔秩相关系数，它也是一种秩相关系数，不过它所计算的对象是分类变量。分类变量可以理解成有类别的变量，可以分为无序的，比如性别（男、女）、血型（A、B、O、AB），以及有序的，比如肥胖等级（重度肥胖，中度肥胖、轻度肥胖、不肥胖）。通常需要求相关性系数的都是有序分类变量。

例子：比如评委对选手的评分（优、中、差等），我们想看两个（或者多个）评委对几位选手的评价标准是否一致；或者医院的尿糖化验报告，想检验各个医院对尿糖的化验结果是否一致，这时候就可以使用肯德尔相关性系数进行衡量。

由于数据情况不同，求得肯德尔相关性系数的计算公式不一样，一般有3种计算公式，在这里就不繁琐地列出计算公式了，具体感兴趣的话可以自行搜寻资料。

R语言计算correlation

x <- c(seq(10))

y <- c(seq(11,20))

res <- cor.test(x, y,method = "pearson") # method 参数修改：“spearman","kendall"

# 具体见 ?cor.test

参考链接：聊聊统计学三大相关性系数