【抓取】6-DOF GraspNet 论文解读

【注】：本文地址：【抓取】6-DOF GraspNet 论文解读

若转载请于明显处标明出处。

前言

这篇关于生成抓取姿态的论文出自英伟达。我在读完该篇论文后我简单地对其进行一些概述，如有错误纰漏请指正！

论文概要

生成抓握姿势是机器人物体操纵任务的关键组成部分。在本工作中，作者提出了抓取生成问题，即使用变分自动编码器对一组抓取进行采样，并利用抓取评估器模型对采样抓取进行评估和微调细化。抓取采样器和抓取refine网络都以深度相机观察到的三维点云作为输入。作者评估了在模拟和现实世界机器人实验中的方法。其方法在具有不同外观、尺度和权重的各种常用对象上获得88%的成功率。作者直接在模拟环境中训练而在现实场景下进行实验测试，这其中没有任何额外的步骤。

整体网络概述

整体网络结构如下图：

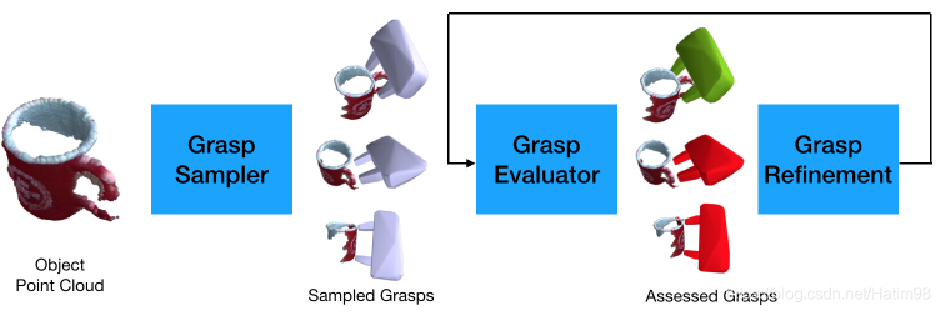
首先，输入三维点云，通过 Grasp Sampler 也就是抓取采样网络，得到多个抓取；然后通过一个 Grasp Evaluater ，评估上一步生成的抓取的成功与否；在评估这一步中，通过 Grasp Refinement 将估计的抓取结果进行微调，使其更贴近于合理抓取，进一步地增大了抓取的成功率。

下面具体来讲一下每一部分。

Variational Grasp Sampler

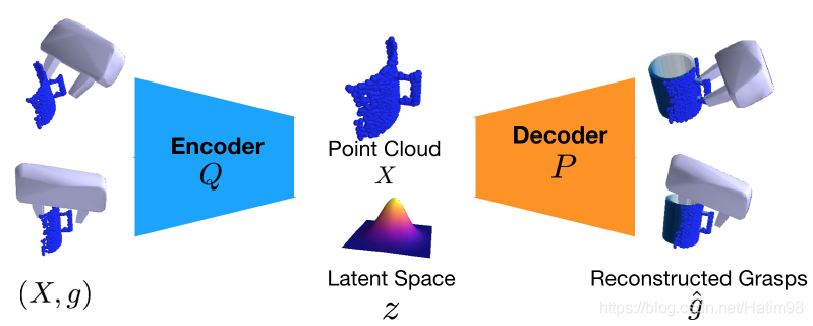
抓取采样网络本质上是一个VAE，也就是变分自编码器。输入 \(X\) 是对原始目标三维点云采样得到的各个视角下的目标点云， \(g\) 其实就是抓取姿态，也就是抓取器在目标坐标系下的 \(R\) 和 \(T\)。通过VAE的编码器Q，将输入编码到隐层空间，得到低维度的隐层变量 \(z\) ，使其满足单位高斯分布；然后再通过对隐层变量 \(z\) 解码，得到与输入相近的 \(g\) 。整个VAE的训练过程就是让z尽量服从上面所说的单位高斯分布，所以在测试的时候，去掉Encoder，直接在单位高斯分布中随机取样，取代了需要编码得到的隐层变量 \(z\) ，再加上输入点云 \(X\) ，就可以得到网络所认为的绝对正确的重建抓取 \(\hat{g}\) 。在训练中，VAE的损失函数如下：

\[\mathcal{L}_{\mathrm{vae}}=\sum_{z \sim Q, g \sim G^{*}} \mathcal{L}(\hat{g}, g)-\alpha \mathcal{D}_{K L}[Q(z \mid X, g), \mathcal{N}(0, I)]
\]

该式采用随机梯度下降优化。对于每个mini-batch，点云 \(X\) 从随机视点观察采样。对于采样点云 \(X\) ，抓取 \(g\) 从Ground Truth集合\(G^{*}\)采用分层采样。

上式中的 \(\mathcal{L}(g, \hat{g})\) 具体式子如下：

\[\mathcal{L}(g, \hat{g})=\frac{1}{n} \sum\|\mathcal{T}(g ; p)-\mathcal{T}(\hat{g} ; p)\|_{1}
\]

此式约束重建抓取与输入抓取相近。 \(\mathcal{T}(\cdot ; p)\) 是机器人夹持器上一组预定义点 \(p\) 的变换，什么意思呢？换句话说就是，在目标坐标系中，把抓取器的模型通过 \(R\) 和 \(T\) 作变换，从而转变为目标坐标系下的抓取器点云。

Grasp Pose Evaluation

因为前一步生成的抓取在网络看来他一定是正确的（因为他认为自己的 \(z\) 服从单位高斯分布，那么从单位高斯分布中取样重建出的 \(\hat{g}\) 一定是正确的抓取），所以实际上要想知道生成的抓取在我们看来是否可行，就还需要加一个判断。因此作者在抓取采样网络之后加了个抓取姿态评估网络。

整个评估网络实质上是一个二分类网络，输入是目标和抓取器的合成渲染点云 \(X \cup X_{g}\) ，输出是成功率 \(s\) 。利用交叉熵损失优化抓取评价网络：

\[\mathcal{L}_{\text {evaluator }}=-(y \log (s)+(1-y) \log (1-s))
\]

式中 \(y\) 是抓取的Ground Truth二进制标签，1/0 代表成功/失败。

在训练中采取了hard negative mining（有翻译叫他难负例挖掘），简单俩说就是建立了一个错题集 \(G^{-}\) ：

\[G^{-}=\left\{g^{-} \mid \exists g \in G^{*}: \mathcal{L}\left(g, g^{-}\right)<\epsilon\right\}
\]

在训练过程中，这个错题集中包含：

从一组预先生成的负抓取中采样 \(g^{-}\) ;
或者通过随机扰动正抓取集 \(G^{*}\) 中的 \(g\) 使夹持器的网格要么与物体网格碰撞，要么将夹持器网格远离物体。

Iterative Grasp Pose Refinement

前面说完了，这一部分我觉得才是重点部分！通过前面的评估，已经得到了一些成功和失败的抓取例子，那么怎么提高成功率呢？换句话说，怎么让估计出来的抓取 \(g\) 更好呢？

为了达到这个目的，作者想到了一个巧妙的办法，既然评估网络中的 \(s\) 越大代表越可能成功，那么使得这些 \(s\) 都尽可能地变大并且趋近于1也就能让抓取 \(g\) 更好了呗~

实际上这就代表了能让 \(s\) 相对于 \(g\) 的函数 \(S\) 值变大的方向。这个方向就是 \(S\) 相对于 \(g\) 的梯度方向，也就得到了下面的式子：

\[\Delta g=\frac{\partial S}{\partial g}=\eta \times \frac{\partial S}{\partial \mathcal{T}(g ; p)} \times \frac{\partial \mathcal{T}(g ; p)}{\partial g}
\]

如果上面不理解，也没关系，有点绕口。我说一个一维曲线的例子。

如上图所示，\(y=f(\theta x)\) 代表拟合出来的曲线，其中 \(\theta\) 代表 \(x\) 的系数（等同于网络的权重参数）。现在假如输入是 \(x_{1}\) ，输出是 \(y_{1}\)，然后我已知 \(y_{2}\) 是一个更好更大的输出值，那么我就需要改变 \(x\) 的值，让 \(x_{1}\) 变成 \(x_{2}\) ：

\[x_{2}=x_{1}+\Delta x
\]

那么变化量 \(\Delta x\) 怎么得到呢？在这个例子里， \(x\) 变化无非两种情况，要么变大要么变小，要想知道我们需要他变大还是变小，只需要让函数 \(f\) 对 \(x\) 求导就得到了斜率，斜率就指明了 \(x\) 变化方向。在这个例子里面 \(x\) 变化方向是 \(x\) 轴的正方向。得到了变化方向我们乘上一个步长 \(\eta\) 就得到了我们需要的变化量 \(\Delta x\) ：

\[\frac{\partial f}{\partial x} \cdot \eta=\Delta x
\]

Experiments

实验部分暂时不说了，作者说这抓取效果就是好反正。其他自对比实验也很有意义，有空再更。